早教吧作业答案频道 -->数学-->
如图,O的内接四边形ABCD两组对边的延长线分别交于点E、F.(1)当∠E=∠F时,则∠ADC=°;(2)当∠A=55°,∠E=30°时,求∠F的度数;(3)若∠E=α,∠F=β,且α≠β.请你用含有α
题目详情
如图, O的内接四边形ABCD两组对边的延长线分别交于点E、F.
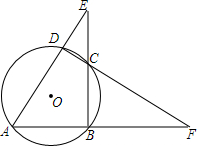
(1)当∠E=∠F时,则∠ADC=___°;
(2)当∠A=55°,∠E=30°时,求∠F的度数;
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.

(1)当∠E=∠F时,则∠ADC=___°;
(2)当∠A=55°,∠E=30°时,求∠F的度数;
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
▼优质解答
答案和解析
(1)∵∠E=∠F,∠DCE=∠BCF,∠ADC=∠E+∠DCE,∠ABC=∠BCF+∠F,
∴∠ADC=∠ABC,
∵四边形ABCD是 O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ADC=90°.
故答案为:90°;
(2)∵在△ABE中,∠A=55°,∠E=30°,
∴∠ABE=180°-∠A-∠E=95°,
∴∠ADF=180°-∠ABE=85°,
∴在△ADF中,∠F=180°-∠ADF-∠A=40°;
(3)∵∠ADC=180°-∠A-∠F,∠ABC=180°-∠A-∠E,
∵∠ADC+∠ABC=180°,
∴180°-∠A-∠F+180°-∠A-∠E=180°,
∴2∠A+∠E+∠F=180°,
∴∠A=
=
.
∴∠ADC=∠ABC,
∵四边形ABCD是 O的内接四边形,
∴∠ADC+∠ABC=180°,
∴∠ADC=90°.
故答案为:90°;
(2)∵在△ABE中,∠A=55°,∠E=30°,
∴∠ABE=180°-∠A-∠E=95°,
∴∠ADF=180°-∠ABE=85°,
∴在△ADF中,∠F=180°-∠ADF-∠A=40°;
(3)∵∠ADC=180°-∠A-∠F,∠ABC=180°-∠A-∠E,
∵∠ADC+∠ABC=180°,
∴180°-∠A-∠F+180°-∠A-∠E=180°,
∴2∠A+∠E+∠F=180°,
∴∠A=
| ∠E+∠F |
| 2 |
| α+β |
| 2 |
看了 如图,O的内接四边形ABCD...的网友还看了以下:
计算题(1)112+(4512-312)÷1124.(2)(856-10.5×45)÷413.(3 2020-04-07 …
某个样本的频数分布直方图中一共有4组,从左到右的组中值依次为5,8,11,14,频数依次为5,4, 2020-04-08 …
(2014•浙江一模)如图为某日不同地点太阳高度(不考虑负值)日变化幅度随纬度变化示意图,一年中, 2020-05-14 …
下列4个数:-2.5,-3,O,1.从大到小排列,正确的是()A.-2.5>-3>0>1B.-3> 2020-05-14 …
一个数的2倍除以5得8余2,求这个数.下面哪个方程是正确的()A.2x÷5=8…2B.5÷2x=8 2020-06-09 …
4.宏定义“#defineDIV(a,b)a/b”,经DIV(x+5,y-5)引用,替换展开后是. 2020-07-10 …
除式7.5÷2.5=3表示()A.7.5能被2.5整除B.2.5能整除7.5C.7.5能被2.5除 2020-07-30 …
(2013•邵阳)“PM2.5”是指大气层中直径小于或等于2.5μm的颗粒物,也称可入肺微粒.它的浓 2020-11-12 …
(2012•六盘水)定义:f(a,b)=(b,a),g(m,n)=(-m,-n).例如f(2,3)= 2020-11-13 …
如图为某日不同地点太阳高度(不考虑负值)日变化幅度随纬度变化示意图,读图回答37~38题.一年中,a 2020-11-27 …