如图，圆O的半径为2，A，B为圆O上的两个定点，且∠AOB=90°，P为优弧AB的中点，设C，D（C在D左侧）为优弧AB上的两个不同的动点，且CD∥BA，记∠POD=α，四边形ABCD的面积为S．（1）求S关于α的

Question

如图，圆O的半径为√(2)，A，B为圆O上的两个定点，且∠AOB=90°，P为优弧AB的中点，设C，D（C在D左侧）为优弧AB上的两个不同的动点，且CD∥BA，记∠POD=α，四边形ABCD的面积为S．

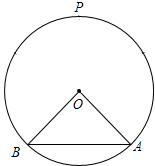
（1）求S关于α的函数关系；
（2）当α为何值时，S取得最大值？并求出S的最大值．

Answer 1

（1）如下图所示：

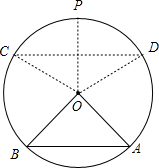
∵圆O的半径为√(2)，A，B为圆O上的两个定点，且∠AOB=90°，
∴AB=√(OB2+OA2)=2，O到AB的距离d=1，
若∠POD=α，则CD=2√(2)sinα，O到CD的距离h=√(2)cosα，
故S=(1)/(2)（2√(2)sinα+2）（√(2)cosα+1）=2sinαcosα+√(2)（sinα+cosα）+1=（sinα+cosα）²+√(2)（sinα+cosα）=2sin²（α+(π)/(4)）+2sin（α+(π)/(4)）．
（2）令t=sin（α+(π)/(4)）．则S=2t²+2t，t∈[(√(2))/(2)，1]，
∵S=2t²+2t的图象是开口朝上，且以直线t=-(1)/(2)为对称的抛物线，
故当t=1，即α=

作业帮用户 2017-04-26

问题解析

（1）求出O到AB和CD的距离，AB与CD的长，代入梯形面积公式，可得S关于α的函数关系；
（2）结合正弦函数的图象和性质及二次函数的图象和性质，可得S的最大值及最大值点．

名师点评

本题考点：

函数解析式的求解及常用方法 函数的最值及其几何意义

考点点评：

本题考查的知识点是函数的解析式的求不地，函数的最值及其几何意义，二次函数的图象和性质，正弦函数的图象和性质，难度中档．

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议

(π)/(4)