早教吧作业答案频道 -->数学-->
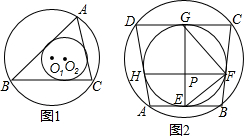
定义:既有外接圆,又有内切圆的凸多边形叫做双圆多边形.如图1,O1是△ABC外接圆,O2是△ABC的内切圆,则△ABC就是双圆三角形.(1)请写出一个双圆四边形的名你;(2)如图2,已知
题目详情
定义:既有外接圆,又有内切圆的凸多边形叫做双圆多边形.如图1, O1是△ABC外接圆, O2是△ABC的内切圆,则△ABC就是双圆三角形.
(1)请写出一个双圆四边形的名你___;
(2)如图2,已知四边形ABCD是双圆四边形,其内切圆与四条边相切于点E,F,G,H,且EG是内切圆的直径,交弦FH于点P,连接EF,FG.
①当∠FGE=40°时,求∠BFE的度数;
②求证:HF⊥GE.
(1)请写出一个双圆四边形的名你___;
(2)如图2,已知四边形ABCD是双圆四边形,其内切圆与四条边相切于点E,F,G,H,且EG是内切圆的直径,交弦FH于点P,连接EF,FG.
①当∠FGE=40°时,求∠BFE的度数;
②求证:HF⊥GE.

▼优质解答
答案和解析
(1)正方形既有外接圆,又有内切圆,所以正方形是双圆四边形,
故答案为正方形.
(2)①如图2中,作直径FM,连接EM,
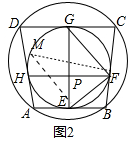
∵FM是直径,
∴∠MEF=90°,
∴∠EMF+∠MFE=90°,
∵BF是切线,
∴MF⊥BF,
∴∠MFB=90°,
∴∠MFE+∠EFB=90°,
∴∠EMF=∠EFB,
∵∠EMF=∠EGF,
∴∠EFB=∠EGF=40°.
②如图3中,连接HG.
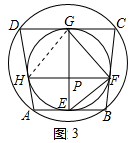
∵四边形ABCD是圆内接四边形,
∴∠D+∠B=180°,
∵H、G、F、E是切点,
∴DG=DH,BF=BE,
∴∠DHG=∠DGH,∠BEF=∠BFE,
∴∠D+2∠DGH=180°,∠B+2∠EFB=180°,
∴2∠DGH+2∠EFB=180°,
∴∠DGH+∠EFB=90°,
由①可知,∠EFB=∠EGF,∠DGH=∠HFG,
∴∠EGF+∠HFG=90°,
∴∠GPE=90°,
∴HF⊥GE.
故答案为正方形.
(2)①如图2中,作直径FM,连接EM,

∵FM是直径,
∴∠MEF=90°,
∴∠EMF+∠MFE=90°,
∵BF是切线,
∴MF⊥BF,
∴∠MFB=90°,
∴∠MFE+∠EFB=90°,
∴∠EMF=∠EFB,
∵∠EMF=∠EGF,
∴∠EFB=∠EGF=40°.
②如图3中,连接HG.

∵四边形ABCD是圆内接四边形,
∴∠D+∠B=180°,
∵H、G、F、E是切点,
∴DG=DH,BF=BE,
∴∠DHG=∠DGH,∠BEF=∠BFE,
∴∠D+2∠DGH=180°,∠B+2∠EFB=180°,
∴2∠DGH+2∠EFB=180°,
∴∠DGH+∠EFB=90°,
由①可知,∠EFB=∠EGF,∠DGH=∠HFG,
∴∠EGF+∠HFG=90°,
∴∠GPE=90°,
∴HF⊥GE.
看了 定义:既有外接圆,又有内切圆...的网友还看了以下:
(本题满分12分)如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D 2020-05-13 …
在正确的读音下面打上“√”。1.老师教同学们画风景。(jiāojiào)2.教室里静悄悄的。(ji 2020-05-15 …
已知BC是O的直径,BF是弦,AD过圆心O,AD⊥BF,AE⊥BC于E,连接FC.(1)如图1,若 2020-05-17 …
请教有关的成语语文题填字,使所填的字前后都构成成语.1.体贴入()不足()听途()长道()兵相接2 2020-05-23 …
给下列汉字选正确读音。1.好事者(A.hǎoB.hào)2.载(A.zǎiB.zài)3.虎大骇( 2020-06-29 …
△ABC内接于O,过点O作OH⊥BC于点H,延长OH交O于点D,连接AD.(1)如图1,求证:∠B 2020-07-09 …
如图,△ABC内接于O,AC为O的直径,PB是O的切线,B为切点,OP⊥BC,垂足为E,交O于D, 2020-07-16 …
如图,△ABC内接于O,过点B作O的切线DE,F为射线BD上一点,连接CF.(1)求证:∠CBE= 2020-07-20 …
如图,AB是O的直径,C是弧AB的中点,连接AC并延长至D,使DC=CA,连接DB,点E为OB的中 2020-07-21 …
大多是课外的1.填颜色,组成语.()装素裹素车()马()气东来灯-酒-半--半--姚--魏--面-耳 2020-11-24 …