早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.(1)求证:△PBQ是等腰直角三角形;
题目详情
如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.
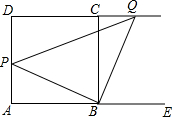
(1)求证:△PBQ是等腰直角三角形;
(2)若PQ2=PB2+PD2+1,求△PAB的面积.

(1)求证:△PBQ是等腰直角三角形;
(2)若PQ2=PB2+PD2+1,求△PAB的面积.
▼优质解答
答案和解析
(1)证明:∵∠QBE=∠PBC,∠QBE+∠QBC=90°,
∴∠PBQ=∠PBC+∠QBC=90°,
∵∠PBC+∠PBA=90°,
∴∠PBA=∠QBC,
在Rt△PAB和Rt△QCB中,
,
∴△PAB≌△QCB(ASA),
∴PB=QB,
∴△PBQ是等腰直角三角形;
(2) 设正方形的边长AB=a,PA=x,
∵△PAB≌△QCB,
∴QC=PA=x,
∴DQ=DC+QC=a+x,PD=AD-PA=a-x,
在Rt△PAB中,PB2=PA2+AB2=x2+a2,
∵PQ2=PB2+PD2+1,
∴(a-x)2+(a+x)2=x2+a2+(a-x)2+1,
解得:2ax=1,
∴ax=
,
∵△PAB的面积S=
PA•PB=
ax=
×
=
.
∴∠PBQ=∠PBC+∠QBC=90°,
∵∠PBC+∠PBA=90°,
∴∠PBA=∠QBC,
在Rt△PAB和Rt△QCB中,
|
∴△PAB≌△QCB(ASA),
∴PB=QB,
∴△PBQ是等腰直角三角形;
(2) 设正方形的边长AB=a,PA=x,
∵△PAB≌△QCB,
∴QC=PA=x,
∴DQ=DC+QC=a+x,PD=AD-PA=a-x,
在Rt△PAB中,PB2=PA2+AB2=x2+a2,
∵PQ2=PB2+PD2+1,
∴(a-x)2+(a+x)2=x2+a2+(a-x)2+1,
解得:2ax=1,
∴ax=
| 1 |
| 2 |
∵△PAB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
看了 如图,在正方形ABCD中,点...的网友还看了以下:
如果等腰三角形的周长是25cm,一腰上的中线把三角形分成两个三角形的周长差是4cm.则这个等腰三角 2020-07-07 …
在具有下列条件的两个等腰三角形中,不能判定它们全等的是[]A.两腰对应相等B.一条腰、底边对应相等 2020-07-13 …
粗声大气的谈话、满口脏话、肆意的大笑、震破屋顶的猜拳、蓬头垢面、衣着不整、随地乱扔垃圾现象等是[] 2020-07-15 …
(2013•香坊区三模)有两个等腰三角形甲和乙,甲的底角等于乙的顶角,甲的底长等于乙的腰长,甲的腰 2020-07-20 …
有两个等腰三角形甲和乙,甲的底角等于乙的顶角,甲的底长等于乙的腰长,甲的腰长等于乙的底长,则甲的底 2020-07-21 …
如图,等腰直角三角形BDC的顶点D在等边三角形ABC的内部,∠BDC=90°,连接AD,过点D作一 2020-07-21 …
下列说法:①顶角相等的两个等腰三角形的底角一定相等;②底边相等的两个等腰三角形全等;③腰长相等且有 2020-07-31 …
已知等腰三角形的周长是25,一腰上的中线把三角形分成两个,两个三角形的周长的差是4.求等腰三角形各 2020-08-03 …
已知等腰三角形的周长是25,一腰上的中线把三角形分成两个,两个三角形的周长的差是4.求等腰三角形各 2020-08-03 …
如果等腰三角形的周长是25cm,一腰上的中线把三角形分成两个三角形的周长差是4cm.则这个等腰三角形 2020-12-01 …