早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠ACB=90°,AC=12cm,BC=4cm,点E从点C出发沿射线CA以每秒3cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.(1)若0<t<4,试问:t为何值
题目详情
如图,在Rt△ABC中,∠ACB=90°,AC=12cm,BC=4cm,点E从点C出发沿射线CA以每秒3cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.
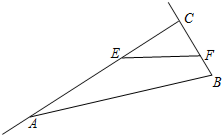
(1)若0<t<4,试问:t为何值时,以E、C、F为顶点的三角形与△ABC相似;
(2)若∠ACB的平分线CG交△ECF的外接圆于点G.
①试说明:当0<t<4时,CE、CF、CG在运动过程中,满足CE+CF=
CG;
②试探究:当t≥4时,CE、CF、CG的数量关系是否发生变化,并说明理由.

(1)若0<t<4,试问:t为何值时,以E、C、F为顶点的三角形与△ABC相似;
(2)若∠ACB的平分线CG交△ECF的外接圆于点G.
①试说明:当0<t<4时,CE、CF、CG在运动过程中,满足CE+CF=
| 2 |
②试探究:当t≥4时,CE、CF、CG的数量关系是否发生变化,并说明理由.
▼优质解答
答案和解析
(1)由题意,EC=3t,BF=t,FC=4-t
∵∠ECF=∠ACB,
∴以E、C、F为顶点的三角形与△ACB相似有两种情况:
当
=
时,△EFC∽△ABC
∴
=
,解得t=2,
当
=
时,△FEC∽△ABC
∴
=
,解得t=0.4.
∴当t=2或0.4秒时,以E、C、F为顶点的三角形与△ABC相似;
(2)①当0<t<4时,
过点G作GH⊥CG交AC于H,如图1:
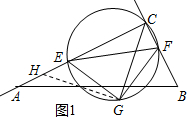
∵∠ACB=90°,
∴EF为△ECF的外接圆的直径,
∴∠EGF=90°,
∴∠EGH=∠FGC,
∵CG平分∠ACB,
∴∠ECG=∠FCG=45°
∴
=
,
∴EG=FG
∵∠ECG=45°,
∴∠EHG=45°,
∴∠EHG=∠FCG,
在△EGH和△FGC中,
,
∴△EGH≌△FGC.
∴EH=FC
∵∠EHG=∠ECG=45°,
∴CH=
CG
∵CH=CE+EH,
∴CE+CF=
CG;
②当t≥4时,
过点G作GM⊥CG交AC于M,如图2:
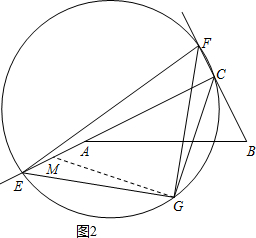
同理可得△EGM≌△FGC.
∴EM=FC
∵∠EMG=∠MCG=45°,
∴CM=
CG
∵CM=CE-EM,
∴CE-CF=
CG.
∵∠ECF=∠ACB,
∴以E、C、F为顶点的三角形与△ACB相似有两种情况:
当
| EC |
| AC |
| FC |
| BC |
∴
| 3t |
| 12 |
| 4-t |
| 4 |
当
| EC |
| BC |
| FC |
| AC |
∴
| 3t |
| 4 |
| 4-t |
| 12 |
∴当t=2或0.4秒时,以E、C、F为顶点的三角形与△ABC相似;
(2)①当0<t<4时,
过点G作GH⊥CG交AC于H,如图1:

∵∠ACB=90°,
∴EF为△ECF的外接圆的直径,
∴∠EGF=90°,
∴∠EGH=∠FGC,
∵CG平分∠ACB,
∴∠ECG=∠FCG=45°
∴
 |
| EG |
 |
| FG |
∴EG=FG
∵∠ECG=45°,
∴∠EHG=45°,
∴∠EHG=∠FCG,
在△EGH和△FGC中,
|
∴△EGH≌△FGC.
∴EH=FC
∵∠EHG=∠ECG=45°,
∴CH=
| 2 |
∵CH=CE+EH,
∴CE+CF=
| 2 |
②当t≥4时,
过点G作GM⊥CG交AC于M,如图2:

同理可得△EGM≌△FGC.
∴EM=FC
∵∠EMG=∠MCG=45°,
∴CM=
| 2 |
∵CM=CE-EM,
∴CE-CF=
| 2 |
看了 如图,在Rt△ABC中,∠A...的网友还看了以下:
刚刚学...(我代我同学问来着..)1.已知直角三角形的两条直角边为a和b.斜边为c.(1)如果a= 2020-03-30 …
有ABC三种烃,已知B完全燃烧的产物n(CO2):n(H2O)=2:3,C为饱和链烃,通常情况下为气 2020-03-31 …
如何确定偏导数极值?例如:已知a,b,c是满足a^2=b^2+c^2的正数,求函数f(a,b,c) 2020-04-26 …
6.酵母菌进行细胞呼吸时,消耗的氧气与释放的二氧化碳比例为1:2时,无氧呼吸所占的比例是 ( ) 2020-05-14 …
(1)如果3x-2/x+1=3+m/x+1则m=-5(2) 如果5x-3/x+2=5+m/x+2则 2020-05-16 …
丙酮酸中C的化合价丙酮酸,分子式为C3H4O3,结构式为CH3COCOOH,如果从分子式出发,O为 2020-06-14 …
比如说将9本书平均分成3组是,C(9,3)C(6,3)C(3,3).那为什么9本书平均分给3个人,是 2020-11-08 …
带“春”字和带的成语(要求“春”字依次在第1.2.3.4.为.如:春意盎然“春”在第1) 2020-12-06 …
三七是中国特有的名贵中药材,喜温暖而荫湿的环境,怕严寒和酷暑,以年平均气温16.0“C~19.3+C 2020-12-06 …
已知:A(2,1),B(4,3),C为坐标轴上的点,且使得ABC是以AB为底边的等腰三角形,请求出C 2021-02-03 …