早教吧作业答案频道 -->数学-->
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.2h,
题目详情
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D位.测得∠DBO=58°,此时B处距离码头O有多远?
(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,精确到1米)
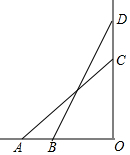
(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,精确到1米)

▼优质解答
答案和解析
设B处距离码头Oxkm,
在Rt△CAO中,∠CAO=45°,
∵tan∠CAO=
,
∴CO=AO•tan∠CAO=(45×0.2+x)•tan45°=9+x,
在Rt△DBO中,∠DBO=58°,
∵tan∠DBO=
,
∴DO=BO•tan∠DBO=x•tan58°,
∵DC=DO-CO,
∴36×0.2=x•tan58°-(9+x),
∴x=
≈27.
因此,B处距离码头O大约27km.
在Rt△CAO中,∠CAO=45°,
∵tan∠CAO=
| CO |
| AO |

∴CO=AO•tan∠CAO=(45×0.2+x)•tan45°=9+x,
在Rt△DBO中,∠DBO=58°,
∵tan∠DBO=
| DO |
| BO |
∴DO=BO•tan∠DBO=x•tan58°,
∵DC=DO-CO,
∴36×0.2=x•tan58°-(9+x),
∴x=
| 36×0.2+9 |
| tan58°-1 |
因此,B处距离码头O大约27km.
看了 如图,轮船甲位于码头O的正西...的网友还看了以下:
游轮甲与游轮乙同时从A.B两个码头相对开出.游轮甲和游轮乙相遇时离A码头1200米,两游轮继续前进 2020-05-13 …
在某段呈直线的江面上从西到东有甲、乙、丙三个码头,某天(非汛期,水流速度可忽略不计)一慢轮与一快轮 2020-06-12 …
海门港和太仓港相距6300米.1号渡轮平均每分行200米,2号渡轮平均每分行220米.这两艘渡轮分 2020-06-28 …
一舰艇和一货轮同时从A港口前往相距100千米的B港口,舰艇和货轮的速度分别为100千米/时和20千 2020-07-04 …
甲乙两个码头相距3500米,一号渡轮每分钟行180米,2号渡轮每分钟行170米,它们往返于两个码头 2020-07-18 …
列方程解应用题2.甲乙两个码头之间的路程是3200米,A,B两艘渡轮分别从两个码头开出,相向而行. 2020-07-18 …
1.某河有相距45千米的上、下两码头,每天定时有甲、乙两艘船速相同的客轮分别从两码头同时出发相向而行 2020-10-30 …
用方程解答并用等量关系式甲乙两艘轮船同时从A码头出发,运送货物到B码头.甲轮船平均每小时航行40千米 2020-11-28 …
轮渡码头到鼓浪屿码头的距离约900米,一艘客轮从轮渡码头驶向鼓浪屿码头用时6分钟,返航时用了5分钟, 2021-01-15 …
轮渡码头到鼓浪屿码头的距离约900米,一艘客轮从轮渡码头驶向鼓浪屿码头用时6分钟,返航时用了5分钟, 2021-01-15 …