早教吧作业答案频道 -->数学-->
小明遇到这样一个问题:如图1,△ABO和△CDO均为等腰直角三角形,∠AOB=∠COD=90°.若△BOC的面积为1,试求以AD,BC,OC+OD的长度为三边长的三角形的面积.小明是这样思考的:要解决这个
题目详情
小明遇到这样一个问题:如图1,△ABO和△CDO均为等腰直角三角形,∠AOB=∠COD=90°.若△BOC的面积为1,试求以AD,BC,OC+OD的长度为三边长的三角形的面积.
小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他的解题思路是延长CO到E,使得OE=CO,连结BE,可证△OBE≌△OAD,从而得到的△BCE即是以AD,BC,OC+OD的长度为三边长的三角形(如图2).
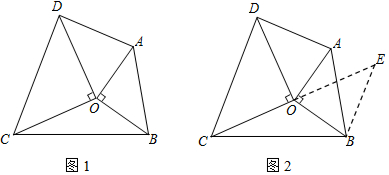
请你回答:图2中△BCE的面积等于___.
小明是这样思考的:要解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他的解题思路是延长CO到E,使得OE=CO,连结BE,可证△OBE≌△OAD,从而得到的△BCE即是以AD,BC,OC+OD的长度为三边长的三角形(如图2).

请你回答:图2中△BCE的面积等于___.
▼优质解答
答案和解析
∵△ABO和△CDO均为等腰直角三角形,∠AOB=∠COD=90°,
∴OD=OC,OA=OB.
又∵∠BOE+∠AOE=90°,∠AOD+∠AOE=90°,
∴∠AOD=∠BOE,
在△OBE和△OAD中,
∵
,
∴△OBE≌△OAD,
∴△BCE即是以AD、BC、OC+OD的长度为三边长的三角形.
∵△OEB与△BOC是等底同高的两个三角形,
∴S△OEB=S△BOC=1,
∴S△BCE=S△OEB+S△BOC=2,
故答案为:2.
∴OD=OC,OA=OB.
又∵∠BOE+∠AOE=90°,∠AOD+∠AOE=90°,
∴∠AOD=∠BOE,
在△OBE和△OAD中,
∵
|
∴△OBE≌△OAD,
∴△BCE即是以AD、BC、OC+OD的长度为三边长的三角形.
∵△OEB与△BOC是等底同高的两个三角形,
∴S△OEB=S△BOC=1,
∴S△BCE=S△OEB+S△BOC=2,
故答案为:2.
看了 小明遇到这样一个问题:如图1...的网友还看了以下:
“梅虽逊雪三分白,雪却输梅一段香。”说明的一个道理是[]A.要看到别人的缺点和不足B.要看到自己的 2020-05-17 …
“梅须逊雪三分白,雪却输梅一段香”这句话主要说明了A:要看到别人的优点跟长处B:要看到梅与雪的差异 2020-05-23 …
自尊是对自己尊严和价值的肯定,是一个人之所以为人的必备操守。一个人要想赢得自尊,就要做到()A.自 2020-06-11 …
人想要听到声音的必备条件是什么?A要有声源B有传播声源的介质C声音的音质要好D耳朵要有听觉觉得A、 2020-07-26 …
2012年一批高官受到党纪国法严处这表明A.任何违法行为都要受到刑罚处罚B.法律只约束国家公职人员 2020-07-29 …
某人买了一张电影票,当他进去时,发现是一座多厅多层电影院,他要找到自己的位置,需要在电影票上找到相关 2020-11-06 …
尊严是立于天地之间的精神支柱.一个人要赢得尊严,就要做到()A.尊重自己,尊重他人B.欣赏自己,轻视 2020-12-03 …
下图漫画《虚惊一场》启示我们()①要做到心中有他人②要增强灾情防范意识③要遵守道德和法律④要加强自我 2020-12-10 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
国务院要求到2020年,在全社会建立起互联互通的诚信系统平台。诚信的基本要求()A.对人守信,对事负 2020-12-17 …