早教吧作业答案频道 -->数学-->
如图,已知点P为∠AOB的角平分线上的一定点,D是射线OA上的一定点,E是OB上的某一点,满足PE=PD,则∠OEP与∠ODP的数量关系是.
题目详情
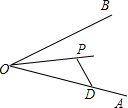
如图,已知点P为∠AOB的角平分线上的一定点,D是射线OA上的一定点,E是OB上的某一点,满足PE=PD,则∠OEP与∠ODP的数量关系是___.

▼优质解答
答案和解析
∠OEP=∠ODP或∠OEP+∠ODP=180°,理由如下: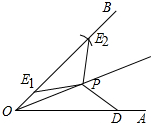
以O为圆心,以OD为半径作弧,交OB于E2,连接PE2,如图所示:
∵在△E2OP和△DOP中,
,
∴△E2OP≌△DOP(SAS),
∴E2P=PD,
即此时点E2符合条件,此时∠OE2P=∠ODP;
以P为圆心,以PD为半径作弧,交OB于另一点E1,连接PE1,
则此点E1也符合条件PD=PE1,
∵PE2=PE1=PD,
∴∠PE2E1=∠PE1E2,
∵∠OE1P+∠E2E1P=180°,
∵∠OE2P=∠ODP,
∴∠OE1P+∠ODP=180°,
∴∠OEP与∠ODP所有可能的数量关系是:∠OEP=∠ODP或∠OEP+∠ODP=180°,
故答案为:∠OEP=∠ODP或∠OEP+∠ODP=180°.

以O为圆心,以OD为半径作弧,交OB于E2,连接PE2,如图所示:
∵在△E2OP和△DOP中,
|
∴△E2OP≌△DOP(SAS),
∴E2P=PD,
即此时点E2符合条件,此时∠OE2P=∠ODP;
以P为圆心,以PD为半径作弧,交OB于另一点E1,连接PE1,
则此点E1也符合条件PD=PE1,
∵PE2=PE1=PD,
∴∠PE2E1=∠PE1E2,
∵∠OE1P+∠E2E1P=180°,
∵∠OE2P=∠ODP,
∴∠OE1P+∠ODP=180°,
∴∠OEP与∠ODP所有可能的数量关系是:∠OEP=∠ODP或∠OEP+∠ODP=180°,
故答案为:∠OEP=∠ODP或∠OEP+∠ODP=180°.
看了 如图,已知点P为∠AOB的角...的网友还看了以下:
帮忙写下论文大纲我写英语论文不知道纲要怎么写题目是中美文化差异的比较—对比家庭教育的找的内容也大部 2020-05-20 …
微积分是关于什么的问题? 2020-06-10 …
英语翻译第一部分是关于财政监督理论的一般研究.本文首先分析了财政监督的涵义,接着分析了相关财政监督 2020-07-04 …
“啊”的七种读音都是怎么读的呢?晚上要考语音学,听说有10分是关于啊的读音的,哪个老师给个答案先呀 2020-07-04 …
SAS与HL的区分是关于全等三角形的(八上第十二章)我不知道该怎么区分HL和SAS, 2020-07-08 …
带分数由和两个部分组成,这两个部分是关系. 2020-07-31 …
跪求关于《青少年与阅读》好句好段,好的追100分!是关于青少年与阅读的,一些好的名言警句或者是关于这 2020-11-04 …
最近新学了二重积分,有个题目是这样的:求一个二重积分,这个积分是关于e的-(y的二次方)先对y积分, 2020-11-24 …
25℃时,重水(D2O)的离子积为1.6×10-15,也可用pH值一样的定义来规定其酸碱度:pD=- 2020-12-05 …
25℃时,重水(D2O)的离子积为1.6×10-15,也可用PH值一样的定义来规定其酸碱度:PD=- 2020-12-17 …