如图，在矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD，则AP的长为（）A.4.8B.32C.5D.33

Question

如图，在矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD，则AP的长为（　　）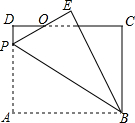

A. 4.8

B. 3

√(2)

C. 5

D. 3

√(3)

Answer 1

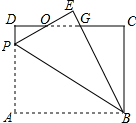如图所示，∵四边形ABCD是矩形，
∴∠D=∠A=∠C=90°，AD=BC=6，CD=AB=8，
根据题意得：△ABP≌△EBP，
∴EP=AP，∠E=∠A=90°，BE=AB=8，
在△ODP和△OEG中，

∠D=∠E

OD=OE

∠DOP=∠EOG

，
∴△ODP≌△OEG（ASA），
∴OP=OG，PD=GE，
∴DG=EP，
设AP=EP=x，则PD=GE=6-x，DG=x，
∴CG=8-x，BG=8-（6-x）=2+x，
根据勾股定理得：BC²+CG²=BG²，
即6²+（8-x）²=（x+2）²，
解得：x=4.8，
∴AP=4.8，
故选：A．