早教吧作业答案频道 -->数学-->
矩形ABCD中,AB=10,BC=8,点P为AD边上的一点,沿直线BP将△ABP翻折至△EBP(点A落在点E处).(1)如图1,当点E落在CD边上,则△EBC的面积S△BEC=;(2)如图2,PE、CD相交于点M,且MD=ME,求折
题目详情
矩形ABCD中,AB=10,BC=8,点P为AD边上的一点,沿直线BP将△ABP翻折至△EBP(点A落在点E处).
(1)如图1,当点E落在CD边上,则△EBC的面积S△BEC=___;
(2)如图2,PE、CD相交于点M,且MD=ME,求折痕BP的长;
(3)如图3,当点P为AD的中点时,连接DE,则图中与∠APB相等的角的个数为___.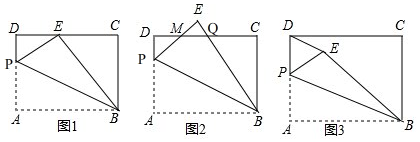
(1)如图1,当点E落在CD边上,则△EBC的面积S△BEC=___;
(2)如图2,PE、CD相交于点M,且MD=ME,求折痕BP的长;
(3)如图3,当点P为AD的中点时,连接DE,则图中与∠APB相等的角的个数为___.

▼优质解答
答案和解析
(1)由折叠知,BE=AB=10,
在Rt△BCE中,BC=8,根据勾股定理得,CE=6,
∴S△BCE=
CE•BC=24,
故答案为24,
(2)如图2,
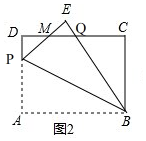
当MD=ME时,设BE交DC与点Q,
在△DPM和△EQM中,
,
∴△DPM≌△EQM
∴DP=EQ DQ=EP,
设AP=x,则DP=8-x=EQ DQ=EP=AP=x
∴CQ=10-x BQ=2+x,
在Rt△CBQ中,由勾股定理得:64+(10-x)2=(x+2)2,
解得x=
,即AP=
,
在Rt△ABP中,由勾股定理得:BP=
,
(3)由折叠知,∠BPE=∠APB,AP=PE,
∵点P是AD中点,
∴AP=DP,
∴PD=PE,
∴∠PDE=∠PED,
∵2∠PDE+∠DPE=180°,2∠APB+∠DPE=180°,
∴∠PDE=∠APB,
∴∠PDE=∠PED=∠BPE=∠APB,
故答案为3.
在Rt△BCE中,BC=8,根据勾股定理得,CE=6,
∴S△BCE=
| 1 |
| 2 |
故答案为24,
(2)如图2,

当MD=ME时,设BE交DC与点Q,
在△DPM和△EQM中,
|
∴△DPM≌△EQM
∴DP=EQ DQ=EP,
设AP=x,则DP=8-x=EQ DQ=EP=AP=x
∴CQ=10-x BQ=2+x,
在Rt△CBQ中,由勾股定理得:64+(10-x)2=(x+2)2,
解得x=
| 20 |
| 3 |
| 20 |
| 3 |
在Rt△ABP中,由勾股定理得:BP=
10
| ||
| 3 |
(3)由折叠知,∠BPE=∠APB,AP=PE,
∵点P是AD中点,
∴AP=DP,
∴PD=PE,
∴∠PDE=∠PED,
∵2∠PDE+∠DPE=180°,2∠APB+∠DPE=180°,
∴∠PDE=∠APB,
∴∠PDE=∠PED=∠BPE=∠APB,
故答案为3.
看了 矩形ABCD中,AB=10,...的网友还看了以下:
按中文意思或给词的适当形式填空.Don"t ____newspapers_____(拿出)of t 2020-05-13 …
请问一下什么叫“谓语动词的分裂现象”?比如这句,Hewilltakemeouttodinnerth 2020-05-14 …
用 speak say talk的适当形式填空“I can write stories,”Lind 2020-05-14 …
1.Every year my parents___(give)me a present for 2020-05-16 …
my mother___________(make)cakes for me yesterday用 2020-05-16 …
用所给词的适当形式填空.1.I___(go)to the cinema.Would you lik 2020-05-16 …
用所给动词的适当形式填空:1、Thank you for ___(ask) us to your 2020-05-16 …
根据句意用所给词的适当形式填空(要翻译)Please write and tell me abou 2020-05-16 …
Could you just ---{tell} him to call me back.【用括号 2020-05-16 …
这个正则表达式怎么写我想查找单词me,但是单词me前面不能有单词by或with.比方:youcan 2020-07-23 …