早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,▱ABCD的顶点的坐标分别为A(-6,9),B(0,9),C(3,0),D(-3,0),抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)过A、B两点,顶点为M.(1)若抛物线过点C,
题目详情
如图,在平面直角坐标系中,▱ABCD的顶点的坐标分别为A(-6,9),B(0,9),C(3,0),D(-3,0),抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)过A、B两点,顶点为M.
(1)若抛物线过点C,求抛物线的解析式;
(2)若抛物线的顶点M落在△ACD的内部(包括边界),求a的取值范围;
(3)若a<0,连结CM交线段AB于点Q(Q不与点B重合),连接DM交线段AB于点P,设S1=S△ADP+S△CBQ,S2=S△MPQ,试判断S1与S2的大小关系,并说明理由.
(1)若抛物线过点C,求抛物线的解析式;
(2)若抛物线的顶点M落在△ACD的内部(包括边界),求a的取值范围;
(3)若a<0,连结CM交线段AB于点Q(Q不与点B重合),连接DM交线段AB于点P,设S1=S△ADP+S△CBQ,S2=S△MPQ,试判断S1与S2的大小关系,并说明理由.
▼优质解答
答案和解析
(1)将点A、B、C的坐标代入抛物线的解析式得:
,
解得:a=-
,b=-2,c=9.
将a=-
,b=-2,c=9代入得y=-
x2-2x+9.
(2)如图1所示:连接AC交直线x=-3与点E.
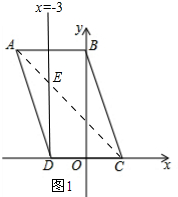
∵点A、B的纵坐标相等,
∴点M在直线x=-3上.
设直线AC的解析式为y=kx+b,将点A、C的坐标代入得:
,
解得:k=-1,b=3.
将k=-1,b=3代入得:y=-x+3.
∵将x=-3代入得;y=-(-3)+3=6.
∴点E的坐标为(-3,6).
设经过点A、B、E三点的抛物线的解析式为y=a(x+3)2+6,将x=0,y=9代入得:9a+6=9.
解得:a=
.
设经过点A、B、D三点的抛物线的解析式为y=a(x+3)2,将x=0,y=9代入得:9a=9.
解得:a=1.
∴
≤a≤1.
(3)如图2所示:当点Q与点B重合时.
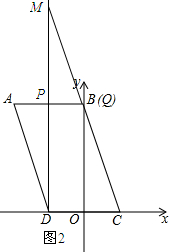
∵DM为抛物线的对称轴,
∴DM是AB的垂直平分线.
∴AP=PB.
∵四边形ABCD为平行四边形,
∴∠A=∠PBM.
在△APD和△BPM中,
,
∴△APD≌△BPM.
∴S△APD=S△PMB.
∵点Q在AB上且与点B不重合,
∴PQ<PB.
∴S△APD>S△PMB.
∴S△ADP+S△CBQ>S△MPQ.
∴S1>S2.
|
解得:a=-
| 1 |
| 3 |
将a=-
| 1 |
| 3 |
| 1 |
| 3 |
(2)如图1所示:连接AC交直线x=-3与点E.

∵点A、B的纵坐标相等,
∴点M在直线x=-3上.
设直线AC的解析式为y=kx+b,将点A、C的坐标代入得:
|
解得:k=-1,b=3.
将k=-1,b=3代入得:y=-x+3.
∵将x=-3代入得;y=-(-3)+3=6.
∴点E的坐标为(-3,6).
设经过点A、B、E三点的抛物线的解析式为y=a(x+3)2+6,将x=0,y=9代入得:9a+6=9.
解得:a=
| 1 |
| 3 |
设经过点A、B、D三点的抛物线的解析式为y=a(x+3)2,将x=0,y=9代入得:9a=9.
解得:a=1.
∴
| 1 |
| 3 |
(3)如图2所示:当点Q与点B重合时.

∵DM为抛物线的对称轴,
∴DM是AB的垂直平分线.
∴AP=PB.
∵四边形ABCD为平行四边形,
∴∠A=∠PBM.
在△APD和△BPM中,
|
∴△APD≌△BPM.
∴S△APD=S△PMB.
∵点Q在AB上且与点B不重合,
∴PQ<PB.
∴S△APD>S△PMB.
∴S△ADP+S△CBQ>S△MPQ.
∴S1>S2.
看了 如图,在平面直角坐标系中,▱...的网友还看了以下:
图一曲线a表示在最适温度、最适pH条件下生成物的量与时间的关系,图二曲线b表示在最适温度、最适pH 2020-06-20 …
关于线圈的自感系数,下面说法正确的是()A.线圈的自感系数越大,自感电动势就一定越大B.线圈中电流等 2020-11-06 …
电冰箱起动时,与电冰箱并联的台灯变暗.关于这一现象.下列说法中正确的是()A.进户线中电流变大B.线 2020-11-08 …
当线圈中的磁通量发生变化时,下列说法中正确的是()A.线圈中一定有感应电流B.线圈中有感应电动势,其 2020-11-21 …
如图中有两根通电直导线,通有如图所示的电流,图(a)中直导线A中通有稳定电流,在右侧放有一圆形导线圈 2020-12-20 …
如图所示,固定长直导线A中通有恒定电流.一个闭合矩形导线框abcd与导线A在同一平面内,并且保持ab 2020-12-22 …
如图所示,固定长直导线A中通有恒定电流.一个闭合矩形导线框abcd与导线A在同一平面内,并且保持ab 2020-12-22 …
如图所示,固定长直导线A中通有恒定电流.一个闭合矩形导线框abcd与导线A在同一平面内,并且保持ab 2020-12-22 …
关于线圈的自感系数,下面说法正确的是()A.线圈的自感系数越大,自感电动势就一定越大B.线圈中电流等 2021-01-29 …
下面说法正确的是()A.线圈中的磁通量变化越大,线圈中产生的感应电动势就越大B.线圈中的磁通量越大, 2021-01-29 …