早教吧作业答案频道 -->数学-->
如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且A1A⊥底面ABCD,点P、Q分别在棱DD1,BC上,BQ=4.(1)若DP=23DD1,证明:PQ∥平面ABB1A1;(2)若P是D1D的中点,证明
题目详情
如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且A1A⊥底面ABCD,点P、Q分别在棱DD1,BC上,BQ=4.
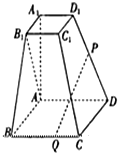
(1)若DP=
DD1,证明:PQ∥平面ABB1A1;
(2)若P是D1D的中点,证明:AB1⊥平面PBC.

(1)若DP=
| 2 |
| 3 |
(2)若P是D1D的中点,证明:AB1⊥平面PBC.
▼优质解答
答案和解析
 证明:(1)在AA1上取一点N,使得AN=
证明:(1)在AA1上取一点N,使得AN=
AA1,
∵DP=
DD1,且A1D1=3,AD=6,
∴PN
AD,又BQ
AD,
∴PN
BQ,
∴四边形BQPN为平行四边形,
∴PQ∥BN,
∵BN⊂平面ABB1A1,PQ⊄ABB1A1.
∴PQ∥ABB1A1.…6分
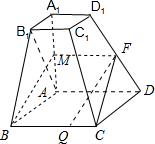
(2)如图所示,取A1A的中点M,连接PM,BM,PC,
∵A1,A,D1D是梯形的两腰,P是D1D的中点,
∴PM∥AD,于是由AD∥BC知,PM∥BC,
∴P,M,B,C四点共面,
由题设可知,BC⊥AB,BC⊥A1A,
∴BC⊥平面ABB1A1,
∴BC⊥AB1,①
∵tan∠ABM=
=
=
=tan∠A1AB1,
∴∠ABM=∠A1AB1,
∴∠ABM+∠BAB1=∠A1AB1+∠BAB1=90°,
∴AB1⊥BM,
再由①与BC∩BM=B,知AB1⊥平面PBC.…12分
 证明:(1)在AA1上取一点N,使得AN=
证明:(1)在AA1上取一点N,使得AN=| 2 |
| 3 |
∵DP=
| 2 |
| 3 |
∴PN
| ∥ |
. |
| 2 |
| 3 |
| ∥ |
. |
| 2 |
| 3 |
∴PN
| ∥ |
. |
∴四边形BQPN为平行四边形,
∴PQ∥BN,
∵BN⊂平面ABB1A1,PQ⊄ABB1A1.
∴PQ∥ABB1A1.…6分
(2)如图所示,取A1A的中点M,连接PM,BM,PC,
∵A1,A,D1D是梯形的两腰,P是D1D的中点,
∴PM∥AD,于是由AD∥BC知,PM∥BC,
∴P,M,B,C四点共面,
由题设可知,BC⊥AB,BC⊥A1A,
∴BC⊥平面ABB1A1,
∴BC⊥AB1,①
∵tan∠ABM=
| AM |
| AB |
| 3 |
| 6 |
| A1B1 |
| A1A |
∴∠ABM=∠A1AB1,
∴∠ABM+∠BAB1=∠A1AB1+∠BAB1=90°,
∴AB1⊥BM,
再由①与BC∩BM=B,知AB1⊥平面PBC.…12分
看了 如图,已知四棱台ABCD-A...的网友还看了以下:
已知命题p,非p和p的否命题一样吗?分别和p同真假吗?命题p:正数的对数都是负数.非p和p的否命题分 2020-03-30 …
ATP的分子简式和18个ATP所具有的高能磷酸键数目分别是[]A.A-P-P~P和18个B.A-P 2020-05-13 …
概率加法公式加法公式,对于任意两事件A,B,有P(A并B)=P(A)+P(B)-P(AB)成立,假 2020-05-16 …
在120°的二面角P-a-Q的两个面P和Q内,分别有点A和点B已知点A和点B到棱a的距离分别为2和 2020-06-13 …
图钉帽的面积为图钉尖的面积的2000倍,若用力F把图钉压入木块,则钉帽与钉尖的压力与压强的大小关系 2020-06-26 …
图钉帽的面积为图钉尖的面积的2000倍,若用力F把图钉压入木块,则钉帽与钉尖的压力与压强的大小关系 2020-06-26 …
研究被测试者的血浆、肾小管以及输尿管中的液体里面P和Q两种物质的浓度,如下表所示,请指出P,Q各是 2020-06-29 …
P是一个光屏,屏上有直径为5厘米的圆孔.Q是一块平面镜,与屏平行放置且相距10厘米.O1、02是过 2020-07-16 …
对于任意二事件A和B,0<P(A)<1,0<P(B)<1,ρ=P(AB)-P(A)P(B)P(A) 2020-08-02 …
(2011•松江区二模)如图所示,甲、乙两个均匀实心正方体放在水平地面上,它们对地面的压强关系为p甲 2020-11-01 …