早教吧作业答案频道 -->数学-->
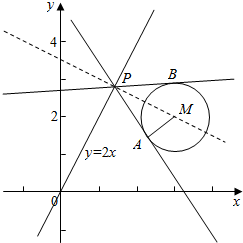
过直线y=2x上一点P作圆M:(x-3)2+(y-2)2=45的两条切线l1,l2,A,B为切点,当直线l1,l2关于直线y=2x对称时,则∠APB等于()A.30°B.45°C.60°D.90°
题目详情
过直线y=2x上一点P作圆M:(x-3)2+(y-2)2=
的两条切线l1,l2,A,B为切点,当直线l1,l2关于直线y=2x对称时,则∠APB等于( )4 5
A. 30°
B. 45°
C. 60°
D. 90°
▼优质解答
答案和解析
 连接PM、AM,可得当切线l1,l2关于直线l对称时,
连接PM、AM,可得当切线l1,l2关于直线l对称时,
直线l⊥PM,且射线PM恰好是∠APB的平分线,
∵圆M的方程为(x-3)2+(y-2)2=
,
∴点M坐标为(3,2),半径r=
,
点M到直线l:2x-y=0的距离为PM=
=
,
由PA切圆M于A,得Rt△PAM中,sin∠APM=
=
,
得∠APM=30°,
∴∠APB=2∠APM=60°.
故选:C.
 连接PM、AM,可得当切线l1,l2关于直线l对称时,
连接PM、AM,可得当切线l1,l2关于直线l对称时,直线l⊥PM,且射线PM恰好是∠APB的平分线,
∵圆M的方程为(x-3)2+(y-2)2=
| 4 |
| 5 |
∴点M坐标为(3,2),半径r=
2
| ||
| 5 |
点M到直线l:2x-y=0的距离为PM=
| |2×3-2| | ||
|
4
| ||
| 5 |
由PA切圆M于A,得Rt△PAM中,sin∠APM=
| AM |
| PM |
| 1 |
| 2 |
得∠APM=30°,
∴∠APB=2∠APM=60°.
故选:C.
看了 过直线y=2x上一点P作圆M...的网友还看了以下:
不用太详细,简要回答就行,(3)曲线y=√2cosx在x=π/4处的切线斜角是?(不用太详细,简要 2020-04-13 …
3/4一3/8十1/5二多少能用简便吗 2020-05-17 …
2.设y=-2e^xsinx,则y'=?3.曲线Y=2X^2+1在点M的瞬时变化率是-4,则M坐标 2020-05-17 …
按1一2一4一3顺序工作的发动机,当一缸压缩到上止点时,二缸活塞处于( ) 行程下止点位置。A.进气 2020-05-31 …
圆纸片最多能切几片?一刀切2块,2刀切4块,3刀切()块?4刀切()块?10块呢?规律呢/? 2020-06-15 …
切饼和切西瓜的问题1)线分割平面:一块薄饼,1刀最多切2块,2刀最多切4块,3刀最多切7块(拜托不 2020-06-15 …
切几刀得计块切一个球体的东西,比如切一刀最多可以得两块,2刀最多4块,3刀最多8块,那么切n刀最多 2020-06-27 …
圣经(箴言24:3-4)3家庭凭智慧建稳,家室靠明辨立定;4因有知识,内室就充满一切贵(箴言24: 2020-07-06 …
用简便方法计算2一|十4一3十6一5十……十200一199 2020-07-18 …
(282+x)÷4一3二x方程式怎么解 2020-07-19 …