早教吧作业答案频道 -->数学-->
如图所示,在平面直角坐标系中xOy中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1
题目详情
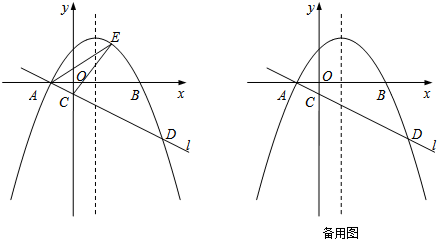
如图所示,在平面直角坐标系中xOy中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)求A、B两点的坐标及抛物线的对称轴;
(2)求直线l的函数表达式(其中k、b用含a的式子表示);
(3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为
,求a的值;
(4)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
(1)求A、B两点的坐标及抛物线的对称轴;
(2)求直线l的函数表达式(其中k、b用含a的式子表示);
(3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为
| 5 |
| 4 |
(4)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.

▼优质解答
答案和解析
 (1)当y=0时,ax2-2ax-3a=0,
(1)当y=0时,ax2-2ax-3a=0,
解得:x1=-1,x2=3,
∴A(-1,0),B(3,0),
对称轴为直线x=
=1;
(2)∵直线l:y=kx+b过A(-1,0),
∴0=-k+b,
即k=b,
∴直线l:y=kx+k,
∵抛物线与直线l交于点A,D,
∴ax2-2ax-3a=kx+k,
即ax2-(2a+k)x-3a-k=0,
∵CD=4AC,
∴点D的横坐标为4,
∴-3-
=-1×4,
∴k=a,
∴直线l的函数表达式为y=ax+a;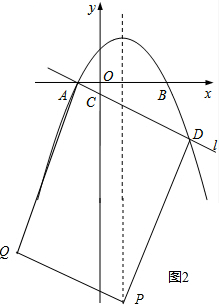
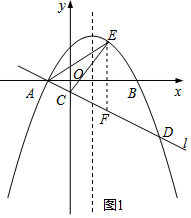
(3)过E作EF∥y轴交直线l于F,设E(x,ax2-2ax-3a),
则F(x,ax+a),EF=ax2-2ax-3a-ax-a=ax2-3ax-4a,
∴S△ACE=S△AFE-S△CEF=
(ax2-3ax-4a)(x+1)-
(ax2-3ax-4a)x=
(ax2-3ax-4a)=
a(x-
)2-
a,
∴△ACE的面积的最大值=-
a,
∵△ACE的面积的最大值为
,
∴-
a=
,
解得a=-
;
(4)以点A、D、P、Q为顶点的四边形能成为矩形,
令ax2-2ax-3a=ax+a,即ax2-3ax-4a=0,
解得:x1=1,x2=4,
∴D(4,5a),
∵抛物线的对称轴为直线x=1,
设P(1,m),
①若AD是矩形ADPQ的一条边,
则易得Q(-4,21a),
m=21a+5a=26a,则P(1,26a),
∵四边形ADPQ是矩形,
∴∠ADP=90°,
∴AD2+PD2=AP2,
∴52+(5a)2+32+(26-5a)2=22+(26a)2,
即a2=
,
∵a<0,
∴a=-
,
∴P(1,-
);
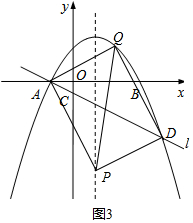
②若AD是矩形APDQ的对角线,
则易得Q(2,-3a),
m=5a-(-3a)=8a,则P(1,8a),
∵四边形APDQ是矩形,
∴∠APD=90°,
∴AP2+PD2=AD2,
∴(-1-1)2+(8a)2+(1-4)+(8a-5a)2=52+(5a)2,
即a2=
,
∵a<0,
∴a=-
,
∴P(1,-4),
综上所述,点A、D、P、Q为顶点的四边形能成为矩形,点P(1,-
 (1)当y=0时,ax2-2ax-3a=0,
(1)当y=0时,ax2-2ax-3a=0,解得:x1=-1,x2=3,
∴A(-1,0),B(3,0),
对称轴为直线x=
| -1+3 |
| 2 |
(2)∵直线l:y=kx+b过A(-1,0),
∴0=-k+b,
即k=b,
∴直线l:y=kx+k,
∵抛物线与直线l交于点A,D,
∴ax2-2ax-3a=kx+k,
即ax2-(2a+k)x-3a-k=0,
∵CD=4AC,
∴点D的横坐标为4,
∴-3-
| k |
| a |
∴k=a,
∴直线l的函数表达式为y=ax+a;

(3)过E作EF∥y轴交直线l于F,设E(x,ax2-2ax-3a),
则F(x,ax+a),EF=ax2-2ax-3a-ax-a=ax2-3ax-4a,
∴S△ACE=S△AFE-S△CEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
∴△ACE的面积的最大值=-
| 25 |
| 8 |
∵△ACE的面积的最大值为
| 5 |
| 4 |
∴-
| 25 |
| 8 |
| 5 |
| 4 |
解得a=-
| 2 |
| 5 |
(4)以点A、D、P、Q为顶点的四边形能成为矩形,
令ax2-2ax-3a=ax+a,即ax2-3ax-4a=0,
解得:x1=1,x2=4,
∴D(4,5a),
∵抛物线的对称轴为直线x=1,
设P(1,m),
①若AD是矩形ADPQ的一条边,
则易得Q(-4,21a),
m=21a+5a=26a,则P(1,26a),
∵四边形ADPQ是矩形,
∴∠ADP=90°,
∴AD2+PD2=AP2,
∴52+(5a)2+32+(26-5a)2=22+(26a)2,
即a2=
| 1 |
| 7 |

∵a<0,
∴a=-
| ||
| 7 |
∴P(1,-
26
| ||
| 7 |
②若AD是矩形APDQ的对角线,
则易得Q(2,-3a),
m=5a-(-3a)=8a,则P(1,8a),
∵四边形APDQ是矩形,
∴∠APD=90°,
∴AP2+PD2=AD2,
∴(-1-1)2+(8a)2+(1-4)+(8a-5a)2=52+(5a)2,
即a2=
| 1 |
| 4 |
∵a<0,
∴a=-
| 1 |
| 2 |
∴P(1,-4),
综上所述,点A、D、P、Q为顶点的四边形能成为矩形,点P(1,-
|
作业帮用户
2017-10-29
|
看了 如图所示,在平面直角坐标系中...的网友还看了以下:
东西半球的分界线是()A.赤道B.20°W与160°E组成的经线圈C.20°E与160°W组成的经 2020-04-23 …
从东西半球来看,中国位于哪个半球?东西半球的分界线是在()A.西半球20°W和160°E经线圈B. 2020-04-23 …
划分东西半球的分界线是()A.赤道B.160°E和20°W组成的经线圈C.0°和180°组成的经线 2020-04-23 …
从东西半球来看,中国位于哪个半球?东西半球的分界线是[]A、西半球20°W和160°E经线圈B、东 2020-04-23 …
面对手中的地球仪,请你解答下面几个问题2~7.东西半球的分界线是()A.西半球20°W和160°E 2020-04-23 …
东西两半球的分界线是()A.0°经线和180°经线组成的经线圈B.20°W和160°E经线组成的经 2020-04-24 …
180°经线说法正确的是A.180°经线与日界线吻合B.180°经线西侧是西十二区,东侧是东十二区 2020-07-14 …
东西半球的分界线是()A.回归线B.赤道C.160°E和20°W的经线圈D.本初子午线 2020-12-05 …
地球上昼夜永远平分的地方是()A.本初子午线上B.北回归线上C.180°经线上D.赤道上 2020-12-22 …
1.下列说法正确的是()A日界线东侧是新的一天的开始B实际上日界线与180度经线重合C从西十二区向东 2021-01-29 …
 扫描下载二维码
扫描下载二维码