早教吧作业答案频道 -->数学-->
如图,点O是△ABC内的一点,AB=AC,∠BAC=90°,∠BOC=120°,将△AOB绕点A按逆时针方向旋转90°得到△ADC,连结OD.(1)求证:△AOD是等腰直角三角形;(2)求证:∠DCO=30°(3)设∠AOB=α,那么
题目详情
如图,点O是△ABC内的一点,AB=AC,∠BAC=90°,∠BOC=120°,将△AOB绕点A按逆时针方向旋转90°得到△ADC,连结OD.
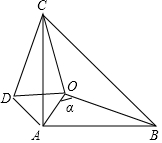
(1)求证:△AOD是等腰直角三角形;
(2)求证:∠DCO=30°
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

(1)求证:△AOD是等腰直角三角形;
(2)求证:∠DCO=30°
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.
▼优质解答
答案和解析
(1)∵△AOB绕点A按逆时针方向旋转90°得到△ADC,
∴AD=AO,∠OAD=∠BAC=90°,
∴△AOD是等腰直角三角形;
(2)∵∠BOC=120°,
∴∠BOA+∠AOC=360°-120°=240°,
由旋转可得,∠AOB=∠ADC,
∴∠ADC+∠AOC=240°,
又∵△AOD是等腰直角三角形,
∴∠DOA=90°,
∴四边形AOCD中,∠DCO=360°-90°-240°=30°;
(3)由题可得,∠COD=360°-∠AOD-∠α-∠COB=360°-45°-∠α-120°=195°-∠α,
∠CDO=∠ADC-∠ADO=∠α-45°,
∠OCD=180°-∠COD-∠CDO=180°-(195°-∠α)-(∠α-45°)=30°,
①若∠COD=∠CDO,即195°-∠α=∠α-45°,
解得:∠α=120°;
②若∠COD=∠OCD,则195°-∠α=30°,
解得:∠α=165°;
③若∠CDO=∠OCD,即∠α-45°=30°,
解得:∠α=75°;
即当α为120°或165°或75°时,△COD是等腰三角形.
∴AD=AO,∠OAD=∠BAC=90°,
∴△AOD是等腰直角三角形;
(2)∵∠BOC=120°,
∴∠BOA+∠AOC=360°-120°=240°,

由旋转可得,∠AOB=∠ADC,
∴∠ADC+∠AOC=240°,
又∵△AOD是等腰直角三角形,
∴∠DOA=90°,
∴四边形AOCD中,∠DCO=360°-90°-240°=30°;
(3)由题可得,∠COD=360°-∠AOD-∠α-∠COB=360°-45°-∠α-120°=195°-∠α,
∠CDO=∠ADC-∠ADO=∠α-45°,
∠OCD=180°-∠COD-∠CDO=180°-(195°-∠α)-(∠α-45°)=30°,
①若∠COD=∠CDO,即195°-∠α=∠α-45°,
解得:∠α=120°;
②若∠COD=∠OCD,则195°-∠α=30°,
解得:∠α=165°;
③若∠CDO=∠OCD,即∠α-45°=30°,
解得:∠α=75°;
即当α为120°或165°或75°时,△COD是等腰三角形.
看了 如图,点O是△ABC内的一点...的网友还看了以下:
某同学设计如下实验装置探究“分子的性质实验”,分析回答问题:(1)图I是按课本进行的一个化学实验, 2020-05-13 …
地图上是按什么,什么绘制的,因此地图上的方向是上北下南左西右东 2020-05-14 …
现有图书两千册,并有红外线扫描枪及图书管理软件,这图书应该如何摆放?如何管理?如何用最简便的方法实 2020-05-17 …
六年级数学题红红紫红红红紫红红红红紫(1)描述一下图形是按什么规律变化的(2)第6个紫后面摆几个红 2020-06-26 …
如图,是按一定规律用火柴棍摆的正方形,如果第n个图形共有100根火柴棍,那么第n个图形中共有个正方 2020-06-27 …
求黑体辐射的辐出度按“频率”分布的曲线大多数图都是按波长分布,而不是按频率.另外,我们老师说两个曲 2020-07-05 …
图中是按照一定规律排列的羊,图(1)有1只羊,图(2)有3只羊,图(3)有10只羊,图(10)有几 2020-07-10 …
下图是一个学操场的平面示意图,它是按照实际的长和宽各缩小到原数的一千分之一,再画出来的,这个操场实 2020-07-20 …
一幅亚洲地图,是按照比亚洲的实地空间距离缩小了5000万倍绘成的.这幅亚洲地图比例尺的正确表示方法是 2020-11-10 …
如图,是按照一定数字规律画出的一行“树型”图.照此规律继续画下去,则图(7)应有的线段条数为. 2020-11-19 …