早教吧作业答案频道 -->数学-->
正方形ABCD内接于O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交O于点F,连接BF、AF,且AF与DE相交于点G.(1)求证:四边形EBFD是矩形;(2)求证:DG=BE;(3)若点E是劣弧AB
题目详情
正方形ABCD内接于 O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交 O于点F,连接BF、AF,且AF与DE相交于点G.
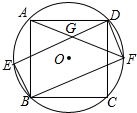
(1)求证:四边形EBFD是矩形;
(2)求证:DG=BE;
(3)若点E是劣弧AB的中点,求tan∠ABE的值.

(1)求证:四边形EBFD是矩形;
(2)求证:DG=BE;
(3)若点E是劣弧AB的中点,求tan∠ABE的值.
▼优质解答
答案和解析
(1)证明:连接BD.
∵四边形ABCD是正方形,
∴∠C=90°,
∴BD是直径,
∴∠BED=∠BFD=90°,
∵DF∥BE,
∴∠DFB+∠EBF=180°,
∴∠EBF=∠BED=∠BFD=90°,
∴四边形EBFD是矩形.
(2) 连接OA.
∵四边形ABCD是正方形,
∴∠AOB=90°,
∴∠DFA=
∠AOB=45°,
∵四边形EBFD是矩形,
∴∠GDF=90°,BE=DF,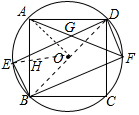
∴∠DGF=∠DFG=45°,
∴DG=DF,
∴DG=BE.
(3) 连接OE交AB于H,设正方形ABCD的边长为2a.
∵
=
,
∴∠AOE=∠BOE=45°,OE⊥AB,
在Rt△AHO中,∵AH=OH=a,
∴OA=
AH=
a,
∴EH=OE-OH=
a-a,
∴tan∠ABE=
=
=
-1.
∵四边形ABCD是正方形,
∴∠C=90°,
∴BD是直径,
∴∠BED=∠BFD=90°,
∵DF∥BE,
∴∠DFB+∠EBF=180°,
∴∠EBF=∠BED=∠BFD=90°,
∴四边形EBFD是矩形.
(2) 连接OA.
∵四边形ABCD是正方形,
∴∠AOB=90°,
∴∠DFA=
| 1 |
| 2 |
∵四边形EBFD是矩形,
∴∠GDF=90°,BE=DF,

∴∠DGF=∠DFG=45°,
∴DG=DF,
∴DG=BE.
(3) 连接OE交AB于H,设正方形ABCD的边长为2a.
∵
 |
| AE |
 |
| BE |
∴∠AOE=∠BOE=45°,OE⊥AB,
在Rt△AHO中,∵AH=OH=a,
∴OA=
| 2 |
| 2 |
∴EH=OE-OH=
| 2 |
∴tan∠ABE=
| EH |
| BH |
| ||
| a |
| 2 |
看了 正方形ABCD内接于O,如图...的网友还看了以下:
一定质量的理想气体的内能E随体积V的变化关系为一直线(其延长线过E~V原点),则此直线表示的过程为 2020-05-14 …
如图表示某地夏季一密闭大棚内一昼夜间CO2浓度的变化。下列能正确表示e点时单位时间内棚内植株消耗的 2020-05-15 …
如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在 2020-06-15 …
如图,在△ABC中,∠A=90°,∠B=60°,AB=3,点D从点A以每秒1个单位长度的速度向点B 2020-07-20 …
如图是人体细胞中两种重要有机物A和E的元素组成及相互关系图,请据图回答:(1)图中⑤与⑥相比,⑤特 2020-07-29 …
(2011•白云区模拟)如图,在直角△ABC内,以A为一个顶点作正方形ADEF,使得点E落在BC边 2020-08-02 …
EXCEL计算k3=1/1+e(2+2.23c3+3d3+2.4e3)这个怎么算k3=1/1+e(2 2020-10-31 …
已知平面内∠CAB,点D,求作:点E,使点E在∠CAB内部,到∠CAB两边的距离相等,且点E到C,D 2020-11-06 …
写作。假如你是李明,你跟你的e-palPaul聊天,他表示学习压力很大,请你给他发封电子邮件,安慰他 2020-11-15 …
(2014•湖南模拟)如图表示一个草原生态系统的食物网,字母A、B、C、D、E、F代表各种生物,x表 2020-12-21 …