早教吧作业答案频道 -->数学-->
如图,已知∠AOB,P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点,(1)要使得△PEF的周长最小,试在图上确定点E、F的位置.(2)若OP=4,要使得△PEF的周长为4,则∠AOB=.
题目详情
如图,已知∠AOB,P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点,
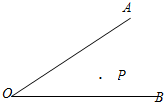
(1)要使得△PEF的周长最小,试在图上确定点E、F的位置.
(2)若OP=4,要使得△PEF的周长为4,则∠AOB=___.

(1)要使得△PEF的周长最小,试在图上确定点E、F的位置.
(2)若OP=4,要使得△PEF的周长为4,则∠AOB=___.
▼优质解答
答案和解析
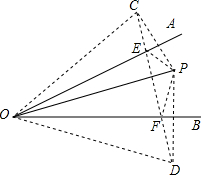 (1)如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
(1)如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
(2)连接OC,OD,PE,PF.
∵点P与点C关于OA对称,
∴OA垂直平分PC,
∴∠COA=∠AOP,PE=CE,OC=OP,
同理,可得∠DOB=∠BOP,PF=DF,OD=OP.
∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB,OC=OD=OP=4,
∴∠COD=2∠AOB.
又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=4,
∴OC=OD=CD=4,
∴△COD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°.
故答案为30°.
 (1)如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
(1)如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.(2)连接OC,OD,PE,PF.
∵点P与点C关于OA对称,
∴OA垂直平分PC,
∴∠COA=∠AOP,PE=CE,OC=OP,
同理,可得∠DOB=∠BOP,PF=DF,OD=OP.
∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB,OC=OD=OP=4,
∴∠COD=2∠AOB.
又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=4,
∴OC=OD=CD=4,
∴△COD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°.
故答案为30°.
看了 如图,已知∠AOB,P是∠A...的网友还看了以下:
已知a.b.c分别是三角形ABC的三个内角A.B.C所对的边,若三角形ABC面积S三角形ABC=2 2020-04-05 …
向量的内积|a+b|前天学的向量的内积,做练习时候第一题的第三问不会,θ=150°是我忘了说a、b 2020-05-14 …
下列命题中,是假命题的是()A.在同一平面内,若a∥b,b∥c,则a∥cB.在同一平面内,若a⊥b 2020-05-17 …
已知△ABC,内角A,B,C所对的边分别为a,b,c,且满足下列三个条件1.a^2+b^2=c^2 2020-05-23 …
若A、B是锐角三角形ABC的两内角...高一数学求解答~~1.若A、B是锐角三角形ABC的两内角, 2020-06-03 …
两道七年级有关有理数的数学题,快,急,十分钟之内,好的追加!1.a=1,b=2,c=-1,化简-3 2020-06-03 …
设a,b是两个实数,A={(x,y)|x=n,y=na+b,n是整数},B={(x,y)|x=m, 2020-06-12 …
怎么判断感应磁场中导体切磁感线电势高低?怎么判断感应磁场中导体切磁感线电势高低?比如说A----- 2020-06-15 …
已知△ABC的内角A,B,C瞒足sin2A+sin(A-B+C)=sin(C-A-B)|+½,面积 2020-06-27 …
已知三角形ABC的内角A,B,C所对应的边分别为a,b,c.且a=1,cosB=3/5(...已知 2020-07-13 …