早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,点A在直线l上,以A为圆心,OA为半径的圆与y轴的另一个交点为E.给出如下定义:若线段OE,A和直线l上分别存在点B,点C和点D,使得四边形ABCD是矩形(点A,B,C,D
题目详情
在平面直角坐标系xOy中,点A在直线l上,以A为圆心,OA为半径的圆与y轴的另一个交点为E.给出如下定义:若线段OE, A和直线l上分别存在点B,点C和点D,使得四边形ABCD是矩形(点A,B,C,D顺时针排列),则称矩形ABCD为直线l的“位置矩形”.
例如,图中的矩形ABCD为直线l的“位置矩形”.
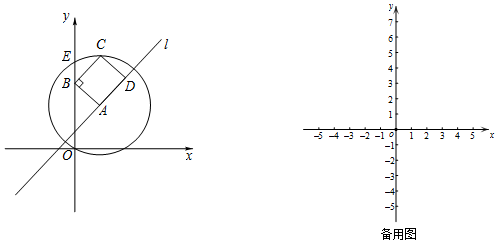
(1)若点A(-1,2),四边形ABCD为直线x=-1的“位置矩形”,则点D的坐标为___;
(2)若点A(1,2),求直线y=kx+1(k≠0)的“位置矩形”的面积;
(3)若点A(1,-3),直线l的“位置矩形”面积的最大值为___,此时点D的坐标为___.
例如,图中的矩形ABCD为直线l的“位置矩形”.
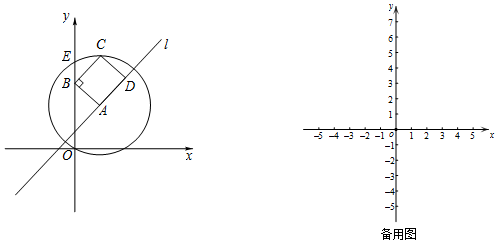
(1)若点A(-1,2),四边形ABCD为直线x=-1的“位置矩形”,则点D的坐标为___;
(2)若点A(1,2),求直线y=kx+1(k≠0)的“位置矩形”的面积;
(3)若点A(1,-3),直线l的“位置矩形”面积的最大值为___,此时点D的坐标为___.
▼优质解答
答案和解析
(1)如图1,
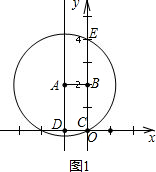
点D的坐标为(-1,0).
故答案为(-1,0);
(2)过点A作AF⊥y轴于点F,连接AO、AC,如图2.
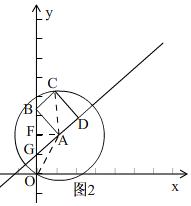
∵点A的坐标为(1,2),
∴AC=AO=
,AF=1,OF=2.
∵点A(1,2)在直线y=kx+1上,
∴k+1=2,
解得k=1.
设直线y=x+1与y轴相交于点G,
当x=0时,y=1,点G(0,1),OG=1,
∴FG=OF-OG=2-1=1=AF,
∴∠FGA=45°,AG=
.
在Rt△GAB中,AB=AG•tan45°=
.
在Rt△ABC中,BC=
=
.
∴所求“位置矩形”ABCD面积为AB•BC=
;
(3)设“位置矩形”的一组邻边长分别为x、y,
则有x2+y2=AC2=AO2=12+32=10.
∵(x-y)2=x2+y2-2xy=10-2xy≥0,
∴xy≤5.
当且仅当x=y时,xy取最大值是5,此时“位置矩形”是正方形.
①当点D在第四象限时,如图3,
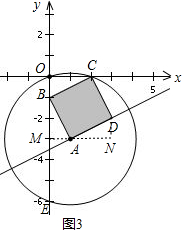
过点A作x轴的平行线,交y轴于点M,交过点D平行于y轴的直线于点N,
∵∠BAM+∠DAN=90°,∠BAM+∠ABM=90°,
∴∠ABM=∠DAN,
在RtAMB和Rt△DNA中,
,
∴RtAMB≌Rt△DNA,
则有AN=BM=2,DN=AM=1,
∴点D的坐标为(1+2,-3+1)即(3,-2).
②当点D在第三象限时,如图4,
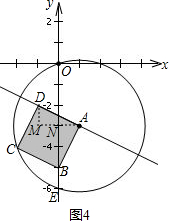
过点A作x轴的平行线,交y轴于点N,交过点D平行于y轴的直线于点M,
同①的方法得:RtANB≌Rt△DMA,
则有DM=AN=1,AM=BN=2,
∴点D的坐标为(1-2,-3+1)即(-1,-2).
故答案为:5、(3,-2)或(-1,-2).

点D的坐标为(-1,0).
故答案为(-1,0);
(2)过点A作AF⊥y轴于点F,连接AO、AC,如图2.
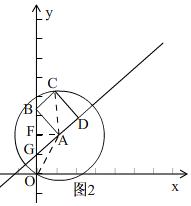
∵点A的坐标为(1,2),
∴AC=AO=
| 5 |
∵点A(1,2)在直线y=kx+1上,
∴k+1=2,
解得k=1.
设直线y=x+1与y轴相交于点G,
当x=0时,y=1,点G(0,1),OG=1,
∴FG=OF-OG=2-1=1=AF,
∴∠FGA=45°,AG=
| 2 |
在Rt△GAB中,AB=AG•tan45°=
| 2 |
在Rt△ABC中,BC=
| AC2-AB2 |
| 3 |
∴所求“位置矩形”ABCD面积为AB•BC=
| 6 |
(3)设“位置矩形”的一组邻边长分别为x、y,
则有x2+y2=AC2=AO2=12+32=10.
∵(x-y)2=x2+y2-2xy=10-2xy≥0,
∴xy≤5.
当且仅当x=y时,xy取最大值是5,此时“位置矩形”是正方形.
①当点D在第四象限时,如图3,

过点A作x轴的平行线,交y轴于点M,交过点D平行于y轴的直线于点N,
∵∠BAM+∠DAN=90°,∠BAM+∠ABM=90°,
∴∠ABM=∠DAN,
在RtAMB和Rt△DNA中,
|
∴RtAMB≌Rt△DNA,
则有AN=BM=2,DN=AM=1,
∴点D的坐标为(1+2,-3+1)即(3,-2).
②当点D在第三象限时,如图4,

过点A作x轴的平行线,交y轴于点N,交过点D平行于y轴的直线于点M,
同①的方法得:RtANB≌Rt△DMA,
则有DM=AN=1,AM=BN=2,
∴点D的坐标为(1-2,-3+1)即(-1,-2).
故答案为:5、(3,-2)或(-1,-2).
看了 在平面直角坐标系xOy中,点...的网友还看了以下:
E是平行四边形ABCD对角线交点,过点A,B,C,D,E分别向直线l引垂线,垂足分别为E是平行四边形 2020-03-31 …
在等腰三角形ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的的任意一点在等腰△ABC中 2020-05-20 …
在等腰三角形△ABC(C为顶点)中,CH是底边上的高线,点P是线段CH上不与端点重和的任意一点,连 2020-06-05 …
直线y=2x=1和直线y=-2x+5分别与y轴交于B.C俩点,俩直线交于A点,D为线段AB的一个动 2020-06-14 …
如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出 2020-06-15 …
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上从点A运动到点B,点 2020-06-19 …
一道八年级角证明详细内容在下面,△ABC的边AB=8cm,AC=4cm,∠A的平分线与BC的垂直平 2020-06-24 …
如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出 2020-08-03 …
已知△ABC中,角C=90度,AB=9,cosA=2/3,把△ABC绕着点C旋转,使得点A落在点D, 2020-11-02 …
如图,点O是线段AB的中点,点C在线段AO上,点D在线段OB上,E,F是线段AB上任意两点如图,点O 2020-12-06 …