早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.(1)判断直线MN与O的位置关系,并说明理由;(2)若OA=4,∠BCM=60°,求图中阴
题目详情
如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
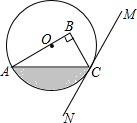
(1)判断直线MN与 O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.

(1)判断直线MN与 O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
▼优质解答
答案和解析
(1)MN是 O切线.
理由: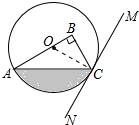 连接OC.
连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,
∴∠BCM=∠BOC,
∵∠B=90°,
∴∠BOC+∠BCO=90°,
∴∠BCM+∠BCO=90°,
∴OC⊥MN,
∴MN是 O切线.
(2)由(1)可知∠BOC=∠BCM=60°,
∴∠AOC=120°,
在RT△BCO中,OC=OA=4,∠BCO=30°,
∴BO=
OC=2,BC=2
∴S阴=S扇形OAC-S△OAC=
-
•4•2
=
-4
.
理由:
 连接OC.
连接OC.∵OA=OC,
∴∠OAC=∠OCA,
∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,
∴∠BCM=∠BOC,
∵∠B=90°,
∴∠BOC+∠BCO=90°,
∴∠BCM+∠BCO=90°,
∴OC⊥MN,
∴MN是 O切线.
(2)由(1)可知∠BOC=∠BCM=60°,
∴∠AOC=120°,
在RT△BCO中,OC=OA=4,∠BCO=30°,
∴BO=
| 1 |
| 2 |
| 3 |
∴S阴=S扇形OAC-S△OAC=
| 120π•42 |
| 360 |
| 1 |
| 2 |
| 3 |
| 16π |
| 3 |
| 3 |
看了 如图,在Rt△ABC中,∠B...的网友还看了以下:
关于神经系统的说法,正确的是()A.脑神经与脊神经分别连接脑和脊髓B.各种神经元的胞体都分布在中枢 2020-06-08 …
关于神经系统的说法,正确的是()A.脑神经与脊神经分别连接脑和脊髓B.各种神经元的胞体都分布在中枢 2020-07-04 …
简答题:(1)“看”与“被看”,是鲁迅小说经常采取的叙述角度,其实质是“吃”与“被吃”。鲁迅小说中 2020-07-21 …
9.城市化是社会经济发展的必然趋势,是社会进步的表现。结合所学知识,回答下列问题。(1)根据图1. 2020-07-22 …
《阿长与山海经》前置作业...1.整体感知课文,说说课文写了哪些事?2.假如阿长是你的保姆,你讨厌 2020-07-29 …
读俄罗斯两大经济地带的划分示意图、俄罗斯两大经济地带的基本经济指标(下表),完成下列要求。(13分) 2020-10-30 …
语言综合运用。《宇宙的边疆》是一篇集科学性与说明性于一体的经典科普作品。请仿照其写法,以“水”为说明 2020-11-21 …
根据你的经历与理解,选择中华民族的一个传统节日,写一段说明性文字。要求:(1)说明顺序合理、清晰;( 2020-12-07 …
2016年1月1日起,我国实施“全面二孩”的生育政策,这说明()A.我国人口已经增长进入负增长时代B 2021-01-14 …
阅读《阿长与<山海经>》一文选段,按完成1—4题。①大概是过于念念不忘了,连阿长也来问《山海经》是怎 2021-01-16 …