早教吧作业答案频道 -->数学-->
(1)如图1,已知△ABC,以AB、AC为边分别向外作正方形ABFD和正方形ACGE,连结BE、CD,猜想BE与CD有什么数量关系?并说明理由;(2)请模仿正方形情景下构造全等三角形的思路,利用构造全
题目详情
(1)如图1,已知△ABC,以AB、AC为边分别向外作正方形ABFD和正方形ACGE,连结BE、CD,猜想BE与CD有什么数量关系?并说明理由;
(2)请模仿正方形情景下构造全等三角形的思路,利用构造全等三角形完成下题:如图2,要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长(结果保留根号).
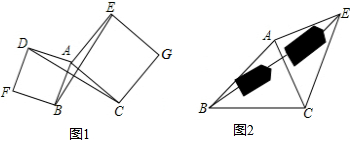
(2)请模仿正方形情景下构造全等三角形的思路,利用构造全等三角形完成下题:如图2,要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长(结果保留根号).

▼优质解答
答案和解析
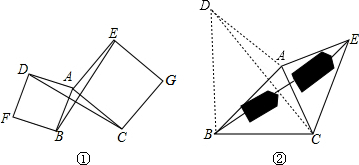 (1)CD=BE.
(1)CD=BE.
理由:如图①∵四边形ABFD和四边形ACGE都是正方形,
∴AD=AB,AC=AE,∠DAB=∠CAE=90°,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE中,
,
∴△ADC≌△ABE(SAS),
∴CD=BE;
(2)如图②,在AB的外侧作AD⊥AB,使AD=AB,连结CD,BD,
∴∠DAB=90°,
∴∠ABD=∠ADB=45°.
∵∠ABC=45°,
∴∠ABD+∠ABC=45°+45°=90°,
即∠DBC=90°.
∴∠CAE=90°,
∴∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE.
在△ADC和△ABE中
,
∴△ADC≌△ABE(SAS),
∴CD=BE.
∵AB=100m,在直角△ABD中,由勾股定理,得
BD=100
.
∴CD=
=100
,
∴BE=CD=100
,
答:BE的长为100
米.
 (1)CD=BE.
(1)CD=BE.理由:如图①∵四边形ABFD和四边形ACGE都是正方形,
∴AD=AB,AC=AE,∠DAB=∠CAE=90°,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE中,
|
∴△ADC≌△ABE(SAS),
∴CD=BE;
(2)如图②,在AB的外侧作AD⊥AB,使AD=AB,连结CD,BD,
∴∠DAB=90°,
∴∠ABD=∠ADB=45°.
∵∠ABC=45°,
∴∠ABD+∠ABC=45°+45°=90°,
即∠DBC=90°.
∴∠CAE=90°,
∴∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE.
在△ADC和△ABE中
|
∴△ADC≌△ABE(SAS),
∴CD=BE.
∵AB=100m,在直角△ABD中,由勾股定理,得
BD=100
| 2 |
∴CD=
1002+(100
|
| 3 |
∴BE=CD=100
| 3 |
答:BE的长为100
| 3 |
看了 (1)如图1,已知△ABC,...的网友还看了以下:
已知RT△ABC中∠C=90°以AB为斜边构造等腰直角三角形∠AOB=90°OA=OB1是说明OC 2020-05-13 …
图为我国东部沿海某地区7月等温线分布示意图,读图回答。(1)试分析造成A、B两地气温差异的原因是什 2020-05-13 …
几道分式方程某商店销售一批服装,每件售价150元,可获利25%,求这种服装的成本价将公式x=a分之 2020-05-22 …
关于等效平衡移动的问题我是一名高中生老师在上课时提到类似于aA(g)=bB(g)+cC(g)解释当 2020-06-28 …
图表示南美洲部分气温及降水分布,读图完成下列要求:(1)大陆东西两侧沿海10℃等温线经过地区的降水量 2020-11-04 …
有利于防止温室效应的有效措施是()①用大量石灰水吸收②减少煤、石油、天然气等化石燃料的燃烧③大力植树 2020-11-04 …
所谓“人造蛋”,就是对豌豆等数百种植物进行试验后筛选出类似鸡蛋的蛋白质等成分,利用生化、食品及烹调技 2020-11-05 …
麦收时节,某些地方仍有就地焚烧麦秸秆的陈规陋习.因焚烧麦秸秆污染了空气而造成的后果有()A.引发火灾 2020-12-24 …
制造一个零件,甲需6分钟,乙需5分钟,丙需4.5分钟.现在有1590个零件的制造任务分配给他们三个人 2020-12-26 …
美国的波音飞机,部分发动机在英国制造,部分尾翼在我国制造。这说明[]A、世界格局出现多极化趋势B、发 2021-01-12 …