早教吧作业答案频道 -->数学-->
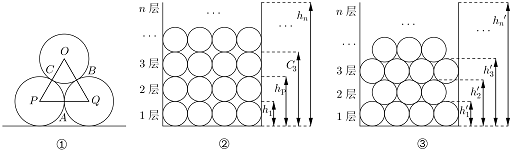
如图①,三个直径为a的等圆P、Q、O两两外切,切点分别是A、B、C.(1)那么OA的长是(用含a的代数式表示);(2)探索:现有若干个直径为a的圆圈分别按如图②所示的方案一和如图③
题目详情
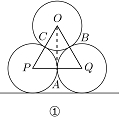
如图①,三个直径为a的等圆 P、 Q、 O两两外切,切点分别是A、B、C.
(1)那么OA的长是___(用含a的代数式表示);
(2)探索:现有若干个直径为a的圆圈分别按如图②所示的方案一和如图③所示的方案二的方式排放,那么这两种方案中n层圆圈的高度hn=___,h′n=___(用含n、a的代数式表示);
(3)应用:现有一种长方体集装箱,箱内长为6米,宽为2.5米,高为2.5米,用这种集装箱装运长为6米,底面直径(横截面的外圆直径)为0.1米的圆柱形铜管,你认为采用第(2)题中的哪种方案在这种集装箱中装运铜管数多?通过计算说明理由;参考数据:
≈1.41,
≈1.73
(1)那么OA的长是___(用含a的代数式表示);
(2)探索:现有若干个直径为a的圆圈分别按如图②所示的方案一和如图③所示的方案二的方式排放,那么这两种方案中n层圆圈的高度hn=___,h′n=___(用含n、a的代数式表示);
(3)应用:现有一种长方体集装箱,箱内长为6米,宽为2.5米,高为2.5米,用这种集装箱装运长为6米,底面直径(横截面的外圆直径)为0.1米的圆柱形铜管,你认为采用第(2)题中的哪种方案在这种集装箱中装运铜管数多?通过计算说明理由;参考数据:
| | 2 |
| | 3 |

▼优质解答
答案和解析
 (1)连接OA,
(1)连接OA,
∵三个直径为a的等圆 P、 Q、 O两两外切,
∴OP=PQ=OQ=a,
∴△OPQ是等边三角形,
∴∠OPQ=60°,
∵AP=AQ,
∴OA⊥PQ,
∴OA=OP•sin60°=
a;
故答案为:
a;
(2)如图②:高度hn=na;
如图③:h′n=
(n-1)a+a;
故答案为:na,
(n-1)a+a;
(3)方案二在这种集装箱中装运铜管数多.
理由:方案一:0.1n≤2.5,
解得:n≤25,
25×25=625.
方案二:根据题意,第一层排放25根,第二层排放24根,
设钢管的放置层数为n,可得
(n-1)×0.1+0.1≤2.5,
解得n≤27.7.
∵n为正整数,
∴n=27.
钢管放置的最多根数为:25×14+24×13=662(根).
∴方案二在这种集装箱中装运铜管数多.
 (1)连接OA,
(1)连接OA,∵三个直径为a的等圆 P、 Q、 O两两外切,
∴OP=PQ=OQ=a,
∴△OPQ是等边三角形,
∴∠OPQ=60°,
∵AP=AQ,
∴OA⊥PQ,
∴OA=OP•sin60°=
| ||
| 2 |
故答案为:
| ||
| 2 |
(2)如图②:高度hn=na;
如图③:h′n=
| ||
| 2 |
故答案为:na,
| ||
| 2 |
(3)方案二在这种集装箱中装运铜管数多.
理由:方案一:0.1n≤2.5,
解得:n≤25,
25×25=625.
方案二:根据题意,第一层排放25根,第二层排放24根,
设钢管的放置层数为n,可得
| ||
| 2 |
解得n≤27.7.
∵n为正整数,
∴n=27.
钢管放置的最多根数为:25×14+24×13=662(根).
∴方案二在这种集装箱中装运铜管数多.
看了 如图①,三个直径为a的等圆P...的网友还看了以下:
如图2-6所示,直线OAC为某一直流电源的总功率P总随电流I变化的图线,抛物线OBC为同一直流电源 2020-04-26 …
有一标有“6V,0.5A”的小型直流电动机,转子是铜导线绕制的线圈组成,阻值约为0.8Ω.现要测量 2020-06-09 …
如图所示是小华同学“研究动滑轮特点”的实验装置.他提起钩码时注意保持测力计竖直匀速移动,测得数据如 2020-06-30 …
定义点P(x0,y0)到直线l:Ax+By+C=0(A2+B2≠0)的有向距离为d=Ax0+By0 2020-07-09 …
英语翻译最近我一直在和我们公司相关部门协调尽快解决现在的问题.事实上重4月开始我一直劝说你们更改付 2020-07-23 …
数学题在平面直角坐标系中,O为坐标原点,已知向量a=(1,2),点A(1,0),B(cosX,T) 2020-08-01 …
1.为什么位移-时间图像和速度-时间图像只能表示直线运动?2.概念中说,只要在运动过程中加速度不变的 2020-12-09 …
物体vt图像是否只表示直线运动vt图像只能表示正反向,是不是画出vt图像已经默认物体已经作直线运动了 2020-12-10 …
如图所示,用伏安法测电阻R0的值时,M、N接在恒压电源上,当S接a点时电压表示数为10V,电流表示数 2021-01-22 …
如图所示,用伏安法测电阻R0的值时,M、N接在恒压电源上,当S接a点时电压表示数为10V,电流表示数 2021-01-22 …