早教吧作业答案频道 -->数学-->
如图,直线AB经过O上的点C,直线AO与O交于点E和点D,OB与O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.(1)求证:①直线AB是O的切线;②∠FDC=∠EDC;(2)求CD的长.
题目详情
如图,直线AB经过 O上的点C,直线AO与 O交于点E和点D,OB与 O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
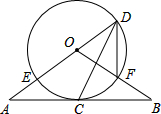
(1)求证:①直线AB是 O的切线;②∠FDC=∠EDC;
(2)求CD的长.

(1)求证:①直线AB是 O的切线;②∠FDC=∠EDC;
(2)求CD的长.
▼优质解答
答案和解析
(1)①证明:连接OC.
∵OA=OB,AC=CB,
∴OC⊥AB,
∵点C在 O上,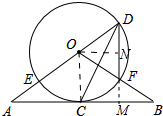
∴AB是 O切线.
②证明:∵OA=OB,AC=CB,
∴∠AOC=∠BOC,
∵OD=OF,
∴∠ODF=∠OFD,
∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,
∴∠BOC=∠OFD,
∴OC∥DF,
∴∠CDF=∠OCD,
∵OD=OC,
∴∠ODC=∠OCD,
∴∠ADC=∠CDF.
(2)作ON⊥DF于N,延长DF交AB于M.
∵ON⊥DF,
∴DN=NF=3,
在RT△ODN中,∵∠OND=90°,OD=5,DN=3,
∴ON=
=4,
∵∠OCM+∠CMN=180°,∠OCM=90°,
∴∠OCM=∠CMN=∠MNO=90°,
∴四边形OCMN是矩形,
∴ON=CM=4,MN=OC=5,
在RT△CDM中,∵∠DMC=90°,CM=4,DM=DN+MN=8,
∴CD=
=
=4
.
∵OA=OB,AC=CB,
∴OC⊥AB,
∵点C在 O上,

∴AB是 O切线.
②证明:∵OA=OB,AC=CB,
∴∠AOC=∠BOC,
∵OD=OF,
∴∠ODF=∠OFD,
∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,
∴∠BOC=∠OFD,
∴OC∥DF,
∴∠CDF=∠OCD,
∵OD=OC,
∴∠ODC=∠OCD,
∴∠ADC=∠CDF.
(2)作ON⊥DF于N,延长DF交AB于M.
∵ON⊥DF,
∴DN=NF=3,
在RT△ODN中,∵∠OND=90°,OD=5,DN=3,
∴ON=
| OD2-DN2 |
∵∠OCM+∠CMN=180°,∠OCM=90°,
∴∠OCM=∠CMN=∠MNO=90°,
∴四边形OCMN是矩形,
∴ON=CM=4,MN=OC=5,
在RT△CDM中,∵∠DMC=90°,CM=4,DM=DN+MN=8,
∴CD=
| DM2+CM2 |
| 82+42 |
| 5 |
看了 如图,直线AB经过O上的点C...的网友还看了以下:
根据所给图A~E,回答下列问题.(1)图A所示遗传信息传递的全过程成为,图B生理过程与图A中相对应 2020-05-02 …
△ABC的边AB=8cm,AC=4cm,∠A的平分线与BC的垂直平分线交宇D点,过D点做DE⊥AB 2020-06-24 …
一道八年级角证明详细内容在下面,△ABC的边AB=8cm,AC=4cm,∠A的平分线与BC的垂直平 2020-06-24 …
如图,△ABC中,AB=6,BC=8,tan∠B=43,点D是边BC上的一个动点(点D与点B不重合 2020-07-20 …
已知菱形ABCD,AB=4,∠B=60°,以点D为圆心作D与直线AB相切于点G,连接DG.(1)求 2020-07-30 …
、已知在三角形ABC中,AB=AC,过点A的直线与三角形ABC的外接圆O于点D,.1、已知在三角形 2020-07-31 …
A、B、C、D、E六人相互握手,到目前为止,A与五人握过手,B与四人握过手,C与三人握过手,D与两人 2020-11-11 …
清除管道铁锈涉及的化学反应,请帮忙写出各物质名称两种方式1)三氧化二铁与过量的甲反应生成A溶液+气体 2020-11-20 …
关于匀速直线运动的速度v=s/t,以下说法中正确的是()A.与通过的路程成正比B.与所用的时间成反比 2020-11-29 …
下图表示葡萄糖跨膜运输的过程,据图分析正确的是()A.该膜中的载体蛋白也能运输氨基酸B.该膜可能是红 2021-01-05 …