早教吧作业答案频道 -->数学-->
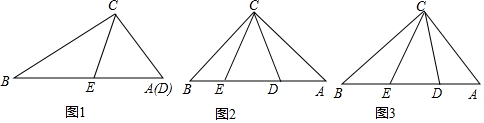
已知:Rt△ABC斜边AB上点D,E,满足∠DCE=45°.(1)如图1,当AC=1,BC=3,且点D与A重合时,求线段BE的长;(2)如图2,当△ABC是等腰直角三角形时,求证:AD2+BE2=DE2;(3)如图3,当AC=3,BC=4时
题目详情
已知:Rt△ABC斜边AB上点D,E,满足∠DCE=45°.
(1)如图1,当AC=1,BC=
,且点D与A重合时,求线段BE的长;
(2)如图2,当△ABC是等腰直角三角形时,求证:AD2+BE2=DE2;
(3)如图3,当AC=3,BC=4时,设AD=x,BE=y,求y关于x的函数关系式,并写出定义域.
(1)如图1,当AC=1,BC=
| 3 |
(2)如图2,当△ABC是等腰直角三角形时,求证:AD2+BE2=DE2;
(3)如图3,当AC=3,BC=4时,设AD=x,BE=y,求y关于x的函数关系式,并写出定义域.

▼优质解答
答案和解析
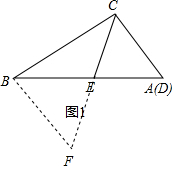 (1)如图1,∵∠ACB=90°,BC=
(1)如图1,∵∠ACB=90°,BC=
,AC=1,
∴AB=2,
过B作BF∥AC交CE的延长线于F,
∴∠F=∠ACE,
∵∠BCA=90°,∠DCE=45°,
∴∠BCE=∠DCE,
∴∠BCE=∠F,
∴BF=BC=
,
∵△BEF∽△AEC,
∴
=
=
,
∴BE=2-
;
(2)证明:过点A作AF⊥AB,使AF=BE,连接DF,CF,
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠FAC=45°,
∴△CAF≌△CBE(SAS),
∴CF=CE,
∠ACF=∠BCE,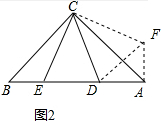
∵∠ACB=90°,∠DCE=45°,
∴∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∵∠ACF=∠BCE,
∴∠ACD+∠ACF=45°,
即∠DCF=45°,
∴∠DCF=∠DCE,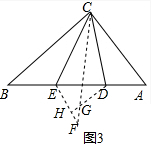
又∵CD=CD,
∴△CDF≌△CDE(SAS),
∴DF=DE,
∵AD2+AF2=DF2,
∴AD2+BE2=DE2;
(3)如图3,作△BCE≌△FCE,△GCD≌△ACD,延长DG交EF于H,
∵∠HFG=∠B,∠HGF=∠CGD=∠A,∠A+∠B=90°,
∴∠DHF=90°,
∵FG=1,∠B=∠F,
∴HF=
,HG=
,
∵EH2+HD2=ED2,
∴(y-
)2+(x+
)2=(5-x-y)2,
∴y=
(0≤x≤
).
 (1)如图1,∵∠ACB=90°,BC=
(1)如图1,∵∠ACB=90°,BC=| 3 |
∴AB=2,
过B作BF∥AC交CE的延长线于F,
∴∠F=∠ACE,
∵∠BCA=90°,∠DCE=45°,
∴∠BCE=∠DCE,
∴∠BCE=∠F,
∴BF=BC=
| 3 |
∵△BEF∽△AEC,
∴
| BE |
| AE |
| BF |
| AC |
| 3 |
∴BE=2-
| 3 |
(2)证明:过点A作AF⊥AB,使AF=BE,连接DF,CF,
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠FAC=45°,
∴△CAF≌△CBE(SAS),
∴CF=CE,
∠ACF=∠BCE,

∵∠ACB=90°,∠DCE=45°,
∴∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∵∠ACF=∠BCE,
∴∠ACD+∠ACF=45°,
即∠DCF=45°,
∴∠DCF=∠DCE,

又∵CD=CD,
∴△CDF≌△CDE(SAS),
∴DF=DE,
∵AD2+AF2=DF2,
∴AD2+BE2=DE2;
(3)如图3,作△BCE≌△FCE,△GCD≌△ACD,延长DG交EF于H,
∵∠HFG=∠B,∠HGF=∠CGD=∠A,∠A+∠B=90°,
∴∠DHF=90°,
∵FG=1,∠B=∠F,
∴HF=
| 4 |
| 5 |
| 3 |
| 5 |
∵EH2+HD2=ED2,
∴(y-
| 4 |
| 5 |
| 3 |
| 5 |
∴y=
| 60-28x |
| 21-5x |
| 15 |
| 7 |
看了 已知:Rt△ABC斜边AB上...的网友还看了以下:
六年级圆与扇形练习题3.如果一个弧长的半径扩大为原来的2倍,圆心角扩大为原来的3倍,则这条弧的长六 2020-05-02 …
8年级数学题:3的n次方+m能被13整除,证明3的n+3次方能被13整除.急用,谢谢刚知道:3^( 2020-05-15 …
matlab数据点怎么作图我有3组长度都不相同的矩阵X,Y,Z如何用他们作图?列如X=[1,2,3 2020-05-16 …
初一下半学期数学练习册题目P14习题12.7(2)(3的1/3次方除以2的1/2次方)的6次方第2 2020-05-23 …
如图3-4如果这个娱乐场所需要有一半以上的绿地,并且它的长与宽之间满足a=3/2b,而小明设计的m 2020-06-25 …
一个梯形,高不变,上底延长3厘米,下底缩短3厘米,形成一个新的梯形.和原来的梯形比,谁大?如果下底 2020-07-10 …
一个长方形的长和宽的比是5:3.如果长方形的长减少5c厘米,宽增加3厘米,这个长方形就变成一个正方 2020-07-16 …
有两个图形重叠部分的面积相当于大长方形面积的13分之2,相当于小长方形面积的10分之3.大长方形与 2020-07-20 …
定义有限数集A中的最大元素与最小元素之差为A的“长度”,如:集合A1={1,2,4}的“长度”为3 2020-08-01 …
1、有两个完全相同的长方体水槽,甲水槽中有水4升,乙水槽中的水是甲水槽现有水的4分之3,如果要使两个 2020-12-03 …