已知.(1)若a=0时,求函数在点(1,)处的切线方程;(2)若函数在[1,2]上是减函数,求实数a的取值范围;(3)令是否存在实数a,当是自然对数的底)时,函数的最小值
已知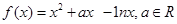 .
.
(1)若a=0时,求函数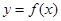 在点(1,
在点(1,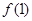 )处的切线方程;
)处的切线方程;
(2)若函数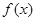 在[1,2]上是减函数,求实数a的取值范围;
在[1,2]上是减函数,求实数a的取值范围;
(3)令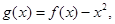 是否存在实数a,当
是否存在实数a,当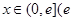 是自然对数的底)时,函数
是自然对数的底)时,函数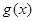 的最小值是3,若存在,求出a的值;若不存在,说明理由.
的最小值是3,若存在,求出a的值;若不存在,说明理由.
(1)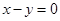
(2)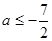
(3)存在实数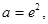 使得
使得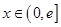 时
时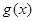 有最小值3
有最小值3
解析 试题分析:
(1)当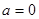 时,
时,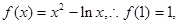 切点
切点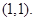
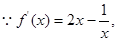
 切线斜率
切线斜率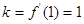
因此,所求切线方程为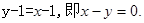
(2)由已知,当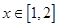 时,
时,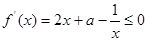 恒成立
恒成立
即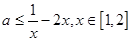 恒成立
恒成立
令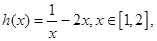 则
则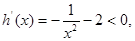 故
故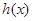 在
在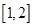 递减。
递减。
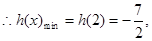 从而
从而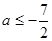
(3)假设存在实数a,使得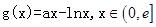 有最小值3
有最小值3
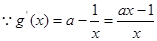
当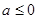 时,
时,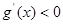 对
对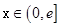 恒成立,
恒成立,
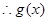 在
在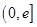 上递减,
上递减,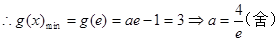
当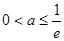 时,
时,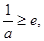
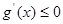 对
对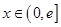 恒成立。
恒成立。
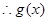 在
在 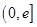 上递减,
上递减,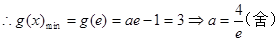
当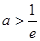 时,
时,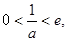
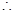 由
由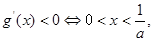 由
由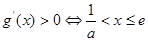
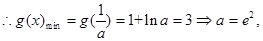 满足条件。
满足条件。
综上,存在实数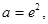 使得
使得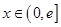 时
时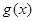 有最小值3
有最小值3
考点:导数的运用
点评:主要是考查了导数在研究函数单调性中的运用,属于中档题。
已知向量a=﹙﹣2,sina﹚,向量b=﹙cosa,1﹚,a∈‐π∕3,π∕61、是否存在a,是向 2020-05-22 …
老师,我的线代基础比较差,是关于您对一个题目给出的解答的.题:设A是n阶矩阵,A=E+xy^T,x 2020-06-19 …
批处理命令求3的n次方怎样表达 2020-06-24 …
设A是n阶矩阵,A=E+xy^T,x与y都是n*1矩阵,且x^T*y=2,求A的特征值、特征向量易 2020-06-30 …
一.设A为3阶方阵,λ1,λ2,λ3是A的三个不同特征值,对应特征向量分别为α1,α2,α3,补充 2020-07-26 …
已知函数f(x)=x平方+x分之2+alnx(x大于0)1.令a=1,求函数f(x)在x=2处的切 2020-07-27 …
f(x)=x^2+ax-lnx令g(x)=f(x)/e^x若函数g(x)在区间(0,1)上是减函数 2020-08-01 …
命题q:y'=1-1/x^2,令y'=0,得x=1或-1(舍)怎么来的?已知a>0,设命题p:函数 2020-08-01 …
对数函数问题(已解出一大半了)设x∈[2,8]函数f(x)=1/2loga(ax)·loga(a^ 2020-08-02 …
已知α1,α2,α3线性无关,若β1=α1+α2,β2=aα2-α3,β3=α1-α2+α3线性相 2020-08-02 …