早教吧作业答案频道 -->数学-->
阅读下面材料:小明遇到这样一个问题:如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明
题目详情
阅读下面材料:
小明遇到这样一个问题:
如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明,若不存在,说明理由.
小明通过探究发现,过点E作AB的垂线EF,垂足为F,能得到一对全等三角形(如图2),从而将解决问题.
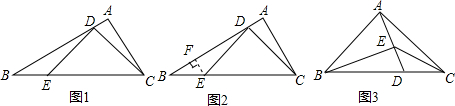
请回答:
(1)小明发现的与CD相等的线段是___.
(2)证明小明发现的结论;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,AB=AC,∠BAC=90°,点D在BC上,BD=2DC,点E在AD上,且∠BEC=135°,求
的值.
小明遇到这样一个问题:
如图1,△ABC中,∠A=90°,∠B=30°,点D,E分别在AB,BC上,且∠CDE=90°.当BE=2AD时,图1中是否存在与CD相等的线段?若存在,请找出并加以证明,若不存在,说明理由.
小明通过探究发现,过点E作AB的垂线EF,垂足为F,能得到一对全等三角形(如图2),从而将解决问题.

请回答:
(1)小明发现的与CD相等的线段是___.
(2)证明小明发现的结论;
参考小明思考问题的方法,解决下面的问题:
(3)如图3,△ABC中,AB=AC,∠BAC=90°,点D在BC上,BD=2DC,点E在AD上,且∠BEC=135°,求
| BE |
| CE |
▼优质解答
答案和解析
(1)DE;
故答案为:DE;
(2)证明:作EF⊥AB,垂足为F.
则∠BFE=∠DFE=90°═∠A═∠CDE.
∵∠ADC+∠CDE=∠ADE=∠DFE+∠FED,
∴∠ADC=∠FED.
∵∠BFE=90°,∠B=30°,
∴BE=2FE.
∵BE=2AD,
∴FE=AD.
在△FED和△ADC中,
∴△FED≌△ADC.
∴DE=CD
(3)如图3,
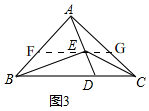
过点E作BC的平行线,与AB、AC分别相交于点F、G.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°.
∵FG∥BC,
∴∠AFG=∠ABC=∠ACB=∠AGF=45°,∠BFE=135°=∠EGC.
∴AF=AG.BF=GC.
∵∠GEC+∠CEB=∠GEB=∠EFB+∠FBE,
∴∠FBE=∠GEC
∴△BFE∽△EGC.
∴
=
=
,
∵FG∥BC,
∴△AFE∽△ABD,△AFG∽△ADC,
∴
=
,
=
,
∴
=
∵BD=2DC,
∴FE=2EG,
∴
=
,
∴
=
,
∴
=
=
故答案为:DE;
(2)证明:作EF⊥AB,垂足为F.
则∠BFE=∠DFE=90°═∠A═∠CDE.
∵∠ADC+∠CDE=∠ADE=∠DFE+∠FED,
∴∠ADC=∠FED.
∵∠BFE=90°,∠B=30°,
∴BE=2FE.
∵BE=2AD,
∴FE=AD.
在△FED和△ADC中,
|
∴△FED≌△ADC.
∴DE=CD
(3)如图3,

过点E作BC的平行线,与AB、AC分别相交于点F、G.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°.
∵FG∥BC,
∴∠AFG=∠ABC=∠ACB=∠AGF=45°,∠BFE=135°=∠EGC.
∴AF=AG.BF=GC.
∵∠GEC+∠CEB=∠GEB=∠EFB+∠FBE,
∴∠FBE=∠GEC
∴△BFE∽△EGC.
∴
| BE |
| CE |
| BF |
| EG |
| FE |
| GC |
∵FG∥BC,
∴△AFE∽△ABD,△AFG∽△ADC,
∴
| FE |
| BD |
| AE |
| AD |
| AE |
| AD |
| EG |
| DC |
∴
| FE |
| BD |
| EG |
| DC |
∵BD=2DC,
∴FE=2EG,
∴
| BF |
| EG |
| 2EG |
| BF |
∴
| BF |
| EG |
| 2 |
∴
| BE |
| CE |
| BF |
| EG |
| 2 |
看了 阅读下面材料:小明遇到这样一...的网友还看了以下:
下列物质充分搅拌后属于溶液的是()A.碳酸钙与水B.油脂与水C.酒精与水D.MnO2与水 2020-05-15 …
可用过滤方法分离的下列列混合物是()A.酒精与水B.大豆油与水C.食盐水与泥沙D.粉笔灰与泥沙 2020-05-17 …
(2014•十堰)下列装置中,与发电机工作原理相同的是()A.甲与乙B.乙与丙C.丙与丁D.甲与丁 2020-06-14 …
有一示数为38.3℃的体温计,没有甩直接用它依次测量体温分别为39℃和37℃的两人的体温,测得的结 2020-06-17 …
历史上的“澶渊之盟”是哪两个政权之间的盟约A.北宋与西夏??????????????????B.北 2020-06-17 …
如图为生物的分类等级示意图.其中亲缘关系最近的是()A.狼与犬B.狼与狮C.猫与虎D.猫与狮 2020-06-19 …
(2014•湖南模拟)虎与狮同属,与猫同科,与狼同目,其中亲缘关系最近的()A.虎与狮B.虎与猫C. 2020-11-10 …
(一)㈡1.人与蛔虫A.互助1.馒头A.维生素2.挖蜜獾与找蜜鸟B.寄生2.西红柿B.脂肪3.狮子与 2020-11-22 …
(一)㈡1.人与蛔虫A.互助1.馒头A.维生素2.挖蜜獾与找蜜鸟B.寄生2.西红柿B.脂肪3.狮子与 2020-12-01 …
华南虎是我国特有的珍稀动物,在分类上属于脊椎动物亚门哺乳纲猫科动物.请问亚门是介于哪两个分类等级单位 2020-12-29 …