早教吧作业答案频道 -->数学-->
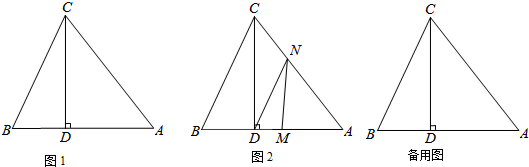
如图1,△ABC中,CD⊥AB于D,且BD:AD:CD=2:3:4,(1)试说明△ABC是等腰三角形;(2)已知S△ABC=10cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A运动,同时动点N从点A出发以相
题目详情
如图1,△ABC中,CD⊥AB于D,且BD:AD:CD=2:3:4,
(1)试说明△ABC是等腰三角形;
(2)已知S△ABC=10cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.
(1)试说明△ABC是等腰三角形;
(2)已知S△ABC=10cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

▼优质解答
答案和解析
(1)设BD=2x,AD=3x,CD=4x,
在Rt△ACD中,AC=
=5x,又AB=5x,
∴AB=AC,
∴△ABC是等腰三角形;
(2)S△ABC=
×5x×4x=10cm2,
解得,x=1cm,
则BD=2cm,AD=3cm,CD=4cm,AC=5cm,
①当MN∥BC时,AM=AN,即5-t=t,
∴t=2.5,
当DN∥BC时,AD=AN,
则t=3,
故若△DMN的边与BC平行时,t值为2.5或3.
②当点M在BD上,即0≤t<2时,△MDE为钝角三角形,但DM≠DE,
当t=2时,点M运动到点D,不构成三角形,
当点M在DA上,即2<t≤5时,△MDE为等腰三角形,有3种可能.
如果DE=DM,则t-2=2.5,
∴t=4.5,
如果ED=EM,则点M运动到点A,
∴t=5,
如果MD=ME=t-2,则(t-2)2-(t-3.5)2=22,
∴t=
,
综上所述,符合要求的t值为4.5或5或
.
在Rt△ACD中,AC=
| AD2+CD2 |
∴AB=AC,
∴△ABC是等腰三角形;
(2)S△ABC=
| 1 |
| 2 |
解得,x=1cm,
则BD=2cm,AD=3cm,CD=4cm,AC=5cm,
①当MN∥BC时,AM=AN,即5-t=t,
∴t=2.5,
当DN∥BC时,AD=AN,
则t=3,
故若△DMN的边与BC平行时,t值为2.5或3.
②当点M在BD上,即0≤t<2时,△MDE为钝角三角形,但DM≠DE,
当t=2时,点M运动到点D,不构成三角形,
当点M在DA上,即2<t≤5时,△MDE为等腰三角形,有3种可能.
如果DE=DM,则t-2=2.5,
∴t=4.5,
如果ED=EM,则点M运动到点A,
∴t=5,
如果MD=ME=t-2,则(t-2)2-(t-3.5)2=22,
∴t=
| 49 |
| 12 |
综上所述,符合要求的t值为4.5或5或
| 49 |
| 12 |
看了 如图1,△ABC中,CD⊥A...的网友还看了以下:
英语语法问题为什么有些以s,x,ch,sh结尾的名词不加es而是s?以o结尾的名词为什么不全加s, 2020-06-08 …
如图所示的四个图形中,∠1和∠2不是同位角的是()A.B.C.D. 2020-07-03 …
急!求解答①关于直线x=-1的轴对称图形中x=1是什么意思②y=2是什么意思急!求解答①关于直线x 2020-07-22 …
下列图形中,∠1与∠2不是同位角的是()A.B.C.D. 2020-07-23 …
如图中的四个图形中,∠1和∠2是同位角的是[]A.②③B.②③④C.①②④D.①④ 2020-07-29 …
如图中的四个图形中,∠1和∠2是同位角的是[]A.②③B.②③④C.①②④D.①④ 2020-07-29 …
下列图形中,∠1与∠2是同位角的是()A.(2)(3)B.(2)(3)(4)C.(1)(2)(4) 2020-07-29 …
三角形中,AE=1/3AC,BD=1/4BC,则阴影三角形ADE的面积阴影和空白三角形ABD和CDE 2020-11-03 …
观察如图,第1个图形中有1个正方形,第2个图形中有3个小正方形,第3个图形中有6个小正方形,…依此规 2021-01-15 …
已知一个n边形中n—1个内角和是1290°哪么这个多边形的另一个内角和是?a30°b90°已知一个n 2021-02-21 …