早教吧作业答案频道 -->数学-->
如图1,已知△ABC是等腰三角形,AB=AC,点D,E分别在AB,AC上,AD=AE.(1)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则DB与CE有何数量关系,请给予证明.(2
题目详情
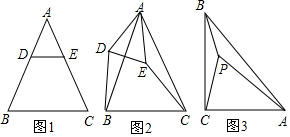
如图1,已知△ABC是等腰三角形,AB=AC,点D,E分别在AB,AC上,AD=AE.
(1)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则DB与CE有何数量关系,请给予证明.
(2)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
(1)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则DB与CE有何数量关系,请给予证明.
(2)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.

▼优质解答
答案和解析
(1)DB=CE.
理由:由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中,
得
,
∴△DAB≌△EAC,
∴DB=CE;
(2)如图,将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2
,
在△PEA中,PE2=(2
)2=8,AE2=12=1,PA2=32=9,
∵PE2+AE2=AP2,
∴△PEA是直角三角形,
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA,
∴∠BPC=∠CEA=135°.
理由:由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中,
得
|
∴△DAB≌△EAC,
∴DB=CE;
(2)如图,将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2
| 2 |
在△PEA中,PE2=(2
| 2 |
∵PE2+AE2=AP2,
∴△PEA是直角三角形,
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA,
∴∠BPC=∠CEA=135°.
看了 如图1,已知△ABC是等腰三...的网友还看了以下:
如图为菜豆种子的结构和种子萌发结构图,请据图回答下列问题:(1)菜豆种子中1、2、4、5的结构共同 2020-05-17 …
该图是美国宇航局2012年7月4日拍摄的太阳活动(耀斑)剧烈爆发图像,大量带电粒子喷射到太空。读图 2020-06-15 …
下面是按照一定规律画出的一列“树型”图:经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3 2020-06-18 …
过去的一年,地球似乎得了重症感冒,喷嚏不止,火山接二连三地喷发。该图“为2010年3月至2011年 2020-06-26 …
下图为荠菜发育中的胚,据图回答:(1)图中[5]是由发育而来的,将发育成具有等器官的植株。(2)图 2020-06-28 …
请根据桃树的相关结构示意图(芽、枝条、花、叶片、果实)回答问题:(1)图一中的③将发育成图二中的. 2020-07-08 …
下列关于叶芽的发育相关说法中,错误的是()A.图甲1是生长点,将来可发育成顶芽B.图甲5可以发育成 2020-07-08 …
将一个正方体(图1)剪开可以展成一些不同的平面图形(图2).其中的图2的(1),(2)都是“带状图” 2020-11-03 …
如图,使一薄钢条的下端固定,分别用不同的力去推它,使其发生如图a、b、c、d所示的形变,图中F1=F 2020-11-07 …
关于PS图,尺寸一样,像素不同,打印出来样子不一样的问题?图A:4.5*2.75inch像素72DP 2020-11-10 …