已知反比例函数的两支图象关于原点对称，利用这一结论解决下列问题：如图，在同一直角坐标系中，正比例函数y=kx的图象与反比例函数y=

Question

已知反比例函数的两支图象关于原点对称，利用这一结论解决下列问题：如图，在同一直角坐标系中，正比例函数y=kx的图象与反比例函数y= (√(3))/(x)的图象分别交于第一、三象限的点B，D，已知点A（-m，O）、C（m，0）．

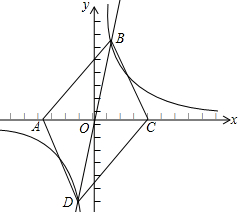
（1）填空：无论k取何值时，四边形ABCD的形状一定是___；
（2）①当点B为（p，1）时，四边形ABCD是矩形，试求p，k，和m的值；
②填空：对①中的m值，能使四边形ABCD为矩形的点B共有___个．
（3）四边形ABCD能不能是菱形？若能，直接写出B点的坐标；若不能，说明理由．

Answer 1

（1）根据对称性可得：OA=OC，OB=OD，则四边形ABCD是平行四边形．
故答案是：平行四边形；
（2）①∵点B（p，1）在y=(√(3))/(x)上，
∴1=(√(3))/(p)，解得p=√(3)．
把B（√(3)，1）代入y=kx得k=(√(3))/(3)．
∵OB²=（√(3)）²+1²=4，
∴OB=2．
∵正比例函数、反比例函数的图象都关于原点对称，
∴OA=OB=OC=2，
∴m=2；
②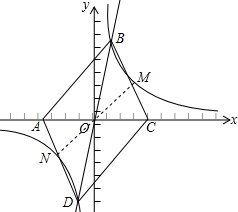作出第一、三象限的角的平分线，交反比例函数图象于点M、N．则MN的解析式是y=x．
当x=m=2时，反比例函数上对应的点是（2，(√(3))/(2)），
直线y=x上对应的点是（2，2）．
∵2>(√(3))/(2)，
∴（2，(√(3))/(2)）在OM的延长线上，即MN<AC．
则能使四边形ABCD是矩形的点B共有2个，
故答案是：2；
（3）四边形ABCD不能是菱形．
理由是：∵A（-m，0）、C（m，0），
∴四边形ABCD的对角线AC在x轴上，
又∵点B、D分别是正比例函数与反比例函数在第一、三象限的交点，
∴对角线BD和AC不可能垂直．
∴四边形ABCD不可能是菱形．