早教吧作业答案频道 -->物理-->
如图所示,一条带有圆轨道的长轨道水平固定,圆轨道竖直,底端分别与两侧的直轨道相切,半径R=0.5m,物块A以V0=6m/s的速度滑入圆轨道,滑过最高点Q,再沿圆轨道滑出后,与直轨上P处静止
题目详情
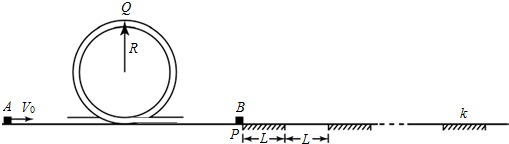
如图所示,一条带有圆轨道的长轨道水平固定,圆轨道竖直,底端分别与两侧的直轨道相切,半径R=0.5m,物块A以V0=6m/s的速度滑入圆轨道,滑过最高点Q,再沿圆轨道滑出后,与直轨上P处静止的物块B碰撞,碰后粘在一起运动.P点左侧轨道光滑,右侧轨道呈粗糙段,光滑段交替排列,每段长度都为L=0.1m.物块与各粗糙段间的动摩擦因数都为μ=0.1,A、B的质量均为m=1kg(重力加速度g取10m/s2;A、B视为质点,碰撞时间极短).
(1)求A滑过Q点时的速度大小V和受到的弹力大小F;
(2)若碰后AB最终停止在第k个粗糙段上,求k的数值;
(3)求碰后AB滑至第n个(n<k)光滑段上的速度VAB与n的关系式.

(1)求A滑过Q点时的速度大小V和受到的弹力大小F;
(2)若碰后AB最终停止在第k个粗糙段上,求k的数值;
(3)求碰后AB滑至第n个(n<k)光滑段上的速度VAB与n的关系式.
▼优质解答
答案和解析
(1)由机械能守恒定律可得:
mv02=mg(2R)+
mv2;
解得:v=4m/s;
由F+mg=m
可得:
F=22N;
(2)AB碰撞前A的速度为vA,由机械能守恒定律可得:
mv02=
mvA2
得vA=v0=6m/s;
AB碰撞后以共同速度vP前进,设向右为正方向,由动量守恒定律可得:
mv0=(m+m)vp
解得:vP=3m/s;
故总动能EK=
(m+m)vP2=
×2×9=9J;
滑块每经过一段粗糙段损失的机械能△EK=fL=μ(m+m)gL=0.1×20×0.1=0.2J;
k=
=
=45;
(3)AB整体滑到第n个光滑段上损失的能量;
E损=nE=0.2nJ
从AB碰撞后运动到第n个光滑段的过程中,由能量守恒定律可得:
(m+m)vP2-
(m+m)vAB2=n△E,
代入解得:vAB=
m/s;
答:1)A滑过Q点时的速度大小V为4m/s;受到的弹力大小F为22N;
(2)k的数值为45;
(3)碰后AB滑至第n个(n<k)光滑段上的速度VAB与n的关系式为vAB=
m/s;
| 1 |
| 2 |
| 1 |
| 2 |
解得:v=4m/s;
由F+mg=m
| v2 |
| R |
F=22N;
(2)AB碰撞前A的速度为vA,由机械能守恒定律可得:
| 1 |
| 2 |
| 1 |
| 2 |
得vA=v0=6m/s;
AB碰撞后以共同速度vP前进,设向右为正方向,由动量守恒定律可得:
mv0=(m+m)vp
解得:vP=3m/s;
故总动能EK=
| 1 |
| 2 |
| 1 |
| 2 |
滑块每经过一段粗糙段损失的机械能△EK=fL=μ(m+m)gL=0.1×20×0.1=0.2J;
k=
| Ek |
| △E |
| 9 |
| 0.2 |
(3)AB整体滑到第n个光滑段上损失的能量;
E损=nE=0.2nJ
从AB碰撞后运动到第n个光滑段的过程中,由能量守恒定律可得:
| 1 |
| 2 |
| 1 |
| 2 |
代入解得:vAB=
| 9-0.2n |
答:1)A滑过Q点时的速度大小V为4m/s;受到的弹力大小F为22N;
(2)k的数值为45;
(3)碰后AB滑至第n个(n<k)光滑段上的速度VAB与n的关系式为vAB=
| 9-0.2n |
看了 如图所示,一条带有圆轨道的长...的网友还看了以下:
看音标写单词:(10分)小题1:['θɜ:sti]小题2:[dʒɜ:ni]小题3:['kʌǀtʃə 2020-05-13 …
matlab:对多项式p=x4+2x3-5x+6和s=x2+2x+31.对多项式p=x4+2x3- 2020-05-17 …
在操作系统中,对信号量S的P原语操作定义中,使进程进入相应等待队列的条件是 ( )。A.S>0 B. 2020-05-23 …
在操作系统中,对信号量S的P原语操作的定义中,使进程进入临界区的条件是A.S>0B.S=0C.S<0 2020-05-23 …
在操作系统中,对信号量S的P原语操作定义中,使进程进入相应等待队列等待的条件是()。A.S>0B.S 2020-05-23 …
在操作系统中,对信号量S的P原语操作定义中,使进程进入相应等待队列等待的条件是______。A.S> 2020-05-23 …
操作系统中,对信号量S的P原语操作定义中,使进程进入相应等待队列等待的条件是( )A.S>0B.S= 2020-05-24 …
操作系统中,对信号量S的P原语操作定义中,使进程进入相应等待队列等待的条件是______。A.S>0 2020-05-24 …
操作系统中,对信号量S的P原语操作定义中,使进程进入相应等待队列等待的条件是()。A.S>0B.S= 2020-05-24 …
操作系统对信号量S的P原语操作定义中,使进程进入相应等待队列的条件是()。A.S≠0B.S<0C.S 2020-05-24 …