在平面直角坐标系中，O为坐标原点，点A（a，a）在第一象限，点B（0，3），点C（c，0），其中0<c<3，∠BAC=90°．（1）根据题意，画出示意图；（2）若a=2，求OC的长；（3）已知点D在线段OC

Question

在平面直角坐标系中，O为坐标原点，点A（a，a）在第一象限，点B（0，3），点C（c，0），其中0<c<3，∠BAC=90°．
（1）根据题意，画出示意图；
（2）若a=2，求OC的长；
（3）已知点D在线段OC上，若OB²-OC²=8S_△CAD，四边形OBAD的面积为(45)/(8)，求a²-a的值．

Answer 1

（1）如图，


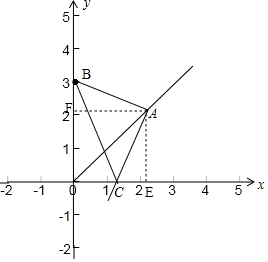
（2）若a=2，则A（2，2），
连接BC，则BC²=c²+9，AC²=（2-c）²+4，AB²=1+4=5，
∵∠BAC=90°，
∴AB²+AC²=BC²，即5+（2-c）²+4=c²+9，
解得：c=1，
即OC=1；

（3）过点A作AE⊥x轴于点E，作AF⊥y轴于点F，
则OF=OE=AF=AE=a，∠AEC=∠AFB=90°，
∵∠CAE+∠ACF=90°，∠BAF+∠CAF=90°，
∴∠CAE=∠BAF，
在△ACE和△ABF中，
∵

∠AEC=∠AFB

∠CAE=∠BAF

AE=AF

，
∴△ACE≌△ABF（AAS），
∴BF=CE=3-a，
∴OC=2a-3，
∵OB²-OC²=8S_△CAD，
∴12a-4a²=8×(1)/(2)×CD×a，
∴CD=3-a，
∴OD=OC-CD=3a-6，
∵S_{四边形OBAD}=S_△OAB+S_△OAD，
∴(45)/(8)=(3)/(2)a+(1)/(2)（3a-6）a，
∴a²-a=(15)/(4)