早教吧作业答案频道 -->数学-->
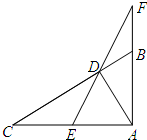
已知在△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC中点,延长ED、AB交于点F.求证:ABAC=DFFA.
题目详情
已知在△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC中点,延长ED、AB交于点F.求证:
=
.
| AB |
| AC |
| DF |
| FA |

▼优质解答
答案和解析
证明:∵∠BAC=90°,AD⊥BC于D,
∴∠BAC=∠ADB=90°,
∴∠BAD+∠ABD=∠ABD+∠C=90°,
∴∠BAD=∠C,
∵E是AC的中点,
∴DE=CE,
∴∠C=∠EDC,
∵∠EDC=∠BDF,
∴∠BAD=∠BDF,
∵∠F=∠F,
∴△DFB∽△AFD,
∴
=
,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠BAD+∠DAC=90°,∠DAC+∠ACD=90°,
∴∠BAD=∠ACD,
∵∠ADB=∠ADC,
∴△ABD∽△CAD;
∴
=
,
∴AB:AC=DF:AF.
∴∠BAC=∠ADB=90°,
∴∠BAD+∠ABD=∠ABD+∠C=90°,
∴∠BAD=∠C,
∵E是AC的中点,
∴DE=CE,
∴∠C=∠EDC,
∵∠EDC=∠BDF,
∴∠BAD=∠BDF,
∵∠F=∠F,
∴△DFB∽△AFD,
∴
| BD |
| AD |
| DF |
| AF |
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠BAD+∠DAC=90°,∠DAC+∠ACD=90°,
∴∠BAD=∠ACD,
∵∠ADB=∠ADC,
∴△ABD∽△CAD;
∴
| AB |
| AC |
| BD |
| AD |
∴AB:AC=DF:AF.
看了 已知在△ABC中,∠BAC=...的网友还看了以下:
提示:D-C=0A-B,A-D,D-C,D-E,E-F=1A-D,C-F=2A-B,D-E,E-F 2020-04-06 …
设栈的初始为空,元素a,b,c,d,e,f,g依次入栈,以下出栈序列不可能出现的是A,a,b,c, 2020-05-17 …
已知A、B、C、D、E、F6种物质的转化关系如下:(1)A+B→C+H2O(2)C+KOH→D↓( 2020-06-05 …
main(){unionEXAMPLE{struct{intx,y;}in;inta,b;}e;e 2020-06-12 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
设一数列a,b,c,d,e,f,通过栈结构不可能不可能排成的顺序数列为()A)c,b,e,f,d, 2020-06-28 …
在五环图案内,分别填写五个数a,b,c,d,e,如图(1),其中a,b,c是三个连续偶数(a<b< 2020-08-02 …
三元一次方程组a*x+b*y+c*z+d=0,e*x+f*y+g*z+h=0,i*x+j*y+k* 2020-08-03 …
多元一次方程求解a=0.1072(a+b+c+d+e)b=0.041(a+b+c+d+e)c=0.2 2020-12-14 …
“我们可以得到A和B分别与C、D、E之间的关系”这句话用英语怎么表达“我们可以得到A和B分别与C、D 2020-12-25 …