我们给出如下定义：若一个四边形有一组对角互补（即对角之和为180°），则称这个四边形为圆满四边形．（1）概念理在平行四边形、菱形、矩形、正方形中，你认为属于圆满四边形的有

Question

我们给出如下定义：若一个四边形有一组对角互补（即对角之和为180°），则称这个四边形为圆满四边形．
（1）概念理 在平行四边形、菱形、矩形、正方形中，你认为属于圆满四边形的有___．
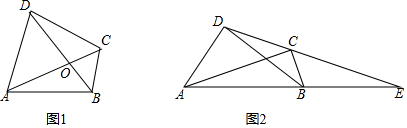
（2）问题探究：如图，在四边形ABCD中，对角线AC、BD相交于点O，若∠ADB=∠ACB，问四边形ABCD是圆满四边形吗？请说明理由．小明经过思考后，判断四边形ABCD是圆满四边形，并提出了如下探究思路：先证明△AOD∽△BOC，得到比例式 (OA)/(OB)= (OD)/(OC)，再证明△AOB∽△DOC，得出对应角相等，根据四边形内角和定理，得出一组对角互补．请你帮助小明写出解题过程．
（3）问题解决：请结合上述解题中所积累的经验和知识完成下题．如图‚，四边形ABCD中，AD⊥BD，AC⊥BC，AB与DC的延长线相交于点E，BE=BD，AB=5，AD=3，求CE的长．

Answer 1

（1）∵矩形和正方形的四个内角都是90°，
∴矩形和正方形的两组对角的和为180°，
∴矩形，正方形是圆满四边形．
故答案是：矩形，正方形；
（2）证明：∵∠ADB=∠ACB，∠AOD=∠BOC，
∴∠DAO=∠CBO，
∴△AOD∽△BOC，
∴(OA)/(OB)=(OD)/(OC)，又∵∠AOB=∠DOC，
∴△AOB∽△DOC，
∴∠OAB=∠ODC，∠OBA=∠OCD．
∴∠ADB+∠ODC+∠OBA+∠OBC=∠ACB+∠OAB+∠OCD+∠OAD=180°，
即∠ADB+∠ABC=∠DCB+∠DAB=180°．
∴四边形ABCD是圆满四边形．

（3）如图‚，∵AD⊥BD，AC⊥BC，
∴∠ADB=∠ACB=90°，
∴四边形ABCD是圆满四边形，
由上可得，∠DAB+∠DCB=∠ADC+∠ABC=180°，∠BDC=∠BAC．
又∵BE=BD，
∴∠BED=∠BDC=∠BAC，
∴AC=EC．
又∵∠BCE+∠DCB=180°，
∴∠BCE=∠DAB，
又∠BEC=∠DEA，
∴△BEC∽△DEA，
∴(EC)/(AE)=(BC)/(AD)，
设AC=EC=x，则BC=√(AB2-AC2)=√(25-x2)
BD=√(AB2-AD2)=4，
∴EA=5+4=9，
∴(√(25-x2))/(3)=(x)/(9)，解得，x=(3√(10))/(2)．
即：CE=(3√(10))/(2)．