在面积为60的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F．若AB=10，BC=12，则CE-CF的值为（）A.2+3B.22+113C.2-3或22-113D.22-113或22+113

Question

在面积为60的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F．若AB=10，BC=12，则CE-CF的值为（　　）

A. 2+

√(3)

B. 22+11

√(3)

C. 2-

√(3)或22-11√(3)

D. 22-11

√(3)或22+11√(3)

Answer 1

分两种情况：①如图1所示：∠A为锐角时；
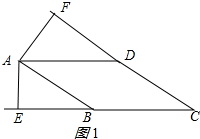
∵平行四边形ABCD的面积=BC•AE=AB•AF=60，AB=10，BC=12，
∴AE=5，AF=6，
∵AE⊥直线BC于点E，作AF⊥直线CD于F，
∴∠AEB=∠AFD=90°，
∴BE=√(102-52)=5√(3)，DF=√(122-62)=6√(3)，
∴CE=12+5√(3)，CF=10+6√(3)，
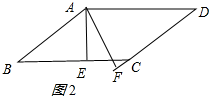
∴CE-CF=2-√(3)；
②如图2所示：∠A为钝角时；
由①得：CE=10-5√(3)，CF=6√(3)-12，
∴CE-CF=22-11√(3)；
故选：C．