空气质量指数（AirQualityIndex，简称AQI）是定量描述空气质量状况的指数，空气质量按照AQI大小分为六级：0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污

Question

空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的指数，空气质量按照AQI大小分为六级：0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污染；>300为严重污染．
一环保人士记录了去年某地某月10天的AQI的茎叶图如图所示．

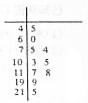
（1）利用该样本估计该地本月空气质量优良（AQI≤100）的天数；（按这个月总共30天计算）
（2）若从样本的空气质量不佳（AQI>100）的这些天中，随机地抽取两天深入分析各种污染指标，求该两天的空气质量等级恰好不同的概率．

Answer 1

（1）由茎叶图可发现样本中空气质量优的天数为1，
空气质量为良的天数为3，故空气质量优良的概率为(1+3)/(10)=(2)/(5)，
故利用该样本估计该地本月空气质量优良的天数为30×(2)/(5)=12；
（2）该样本中轻度污染共4天，分别记为a，b，c，d，
中度污染为1天，记为A，重度污染为1天，记为α，
则从中随机抽取2天的所有可能结果为：（a，b）（a，c）
（a，d）（a，A）（A，α）（b，c）（b，d）（b，A）
（b，α）（c，d）（c，A）（c，α）（d，A）（d，α）
（A，α）共15个，其中空气质量等级恰好不同有（a，A）（A，α）（b，A）
（b，α）（c，A）（c，α）（d，A）（d，α）（A，α）共9个，
该两天的空气质量等级恰好不同的概率P=(9)/(15)=(3)/(5)