早教吧作业答案频道 -->数学-->
如图,平面直角坐标系中,A(2,0),△OAC为等边三角形.(1)如图1,若D(0,4),△ADE为等边三角形,∠DAC=10°,求∠AEC的度数.(2)如图2,若P为x轴正半轴上一点,且P在A的右侧,△PCM
题目详情
如图,平面直角坐标系中,A(2,0),△OAC为等边三角形.
(1)如图1,若D(0,4),△ADE为等边三角形,∠DAC=10°,求∠AEC的度数.
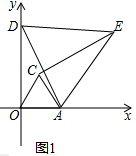
(2)如图2,若P为x轴正半轴上一点,且P在A的右侧,△PCM为等边三角形,MA的延长线交y轴于N,求AM-AP的值.
(3)如图3,若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F,求证:AF+MF=PF.
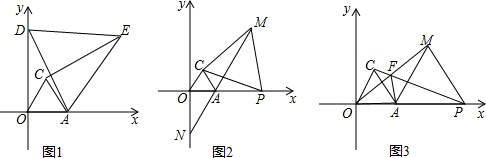
(1)如图1,若D(0,4),△ADE为等边三角形,∠DAC=10°,求∠AEC的度数.
(2)如图2,若P为x轴正半轴上一点,且P在A的右侧,△PCM为等边三角形,MA的延长线交y轴于N,求AM-AP的值.
(3)如图3,若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F,求证:AF+MF=PF.

▼优质解答
答案和解析
 (1) 如图1,∵△AOC和△DAE是等边三角形,
(1) 如图1,∵△AOC和△DAE是等边三角形,
∴AC=AO,AE=AD,∠OAC=∠EAD=60°
∴∠CAE=∠DAO=60○-∠CAD,
在△CAE和△OAD中,
,
∴△CAE≌△OAD(SAS),
∴CE=OD=4,∠ACE=∠AOD=90°,
∵∠DAC=10°,∠DAE=60°,
∴∠CAE=60°+10°=70°,
∴∠AEC=180°-90°-70°=20°;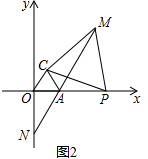
(2) 如图2,∵△AOC和△CPM是等边三角形,
∴OA=AC,CP=CM,∠OCA=∠MCP=60°,
∴∠OCP=∠ACM,
在△OCP和△ACM中,
,
∴△OCP≌△ACM(SAS),
∴AM=OP,
∴AM-OP=OP-AP=OA,
∵A(2,0),
∴OA=2,
即AM-AP=2;
(3)证明:如图3,将△PAF顺时针旋转60°得到△EAM,
则△PAF≌△MAE,∠FAE=60°,
∴PF=EM,AF=AE,
∴△EAF是等边三角形,
∴EF=AF,
∴AF+MF=EF+MF=EM=PF,即AF+MF=PF.
 (1) 如图1,∵△AOC和△DAE是等边三角形,
(1) 如图1,∵△AOC和△DAE是等边三角形,∴AC=AO,AE=AD,∠OAC=∠EAD=60°
∴∠CAE=∠DAO=60○-∠CAD,
在△CAE和△OAD中,
|
∴△CAE≌△OAD(SAS),
∴CE=OD=4,∠ACE=∠AOD=90°,
∵∠DAC=10°,∠DAE=60°,
∴∠CAE=60°+10°=70°,
∴∠AEC=180°-90°-70°=20°;

(2) 如图2,∵△AOC和△CPM是等边三角形,
∴OA=AC,CP=CM,∠OCA=∠MCP=60°,
∴∠OCP=∠ACM,
在△OCP和△ACM中,
|
∴△OCP≌△ACM(SAS),
∴AM=OP,
∴AM-OP=OP-AP=OA,
∵A(2,0),
∴OA=2,
即AM-AP=2;

(3)证明:如图3,将△PAF顺时针旋转60°得到△EAM,
则△PAF≌△MAE,∠FAE=60°,
∴PF=EM,AF=AE,
∴△EAF是等边三角形,
∴EF=AF,
∴AF+MF=EF+MF=EM=PF,即AF+MF=PF.
看了 如图,平面直角坐标系中,A(...的网友还看了以下:
智解字谜1.高小姐探头相望,李小姐半露半藏,郑小姐侧着耳朵听详细.()2.半边生鳞不生角,半边生角不 2020-03-30 …
1.高小姐探头相望,李小姐半露半藏,郑小姐侧着耳朵提听端详.()2.半边生鳞不生角,半边生角不生鳞, 2020-03-30 …
1.高小姐探头相望,李小姐半露半藏,郑小姐侧着耳朵听端详.()2.半边生鳞不生角,半边生角不生鳞,半 2020-03-30 …
1、半边阴,半边阳;半边热,半边凉.2、一边软,一边硬;软做衣,硬砌墙.3、买棵菜,拿回家;添一笔 2020-05-13 …
猜一谜语,三个谜语的答案都是一样的1.我有一物生得巧,半边鳞甲半边毛;半边离水难活命,半边入水命难 2020-06-20 …
帮忙猜猜字谜1,高小姐探头相望,李小姐半露半藏,郑小姐侧着耳朵听端详.()2.半边生磷不生角,半边 2020-06-23 …
1.高小姐探头想望,李小姐半露半藏,郑小姐侧着耳朵听端详.()2.半边生鳞不生角,半边生角不生鳞, 2020-06-26 …
1,智解字谜(1)高小姐探头相望,李小姐半露半藏,邓小姐侧着耳朵听端详.()(2)半边生鳞不生角, 2020-07-02 …
绕口令大集合,你能闯到第几关?1,半边莲,莲半边,半边莲长在山涧边。半边天路过山涧边,发现这片半边 2020-07-25 …
帮忙猜猜字谜1,高小姐探头相望,李小姐半露半藏,郑小姐侧着耳朵听端详.()2.半边生磷不生角,半边生 2021-01-04 …