早教吧作业答案频道 -->数学-->
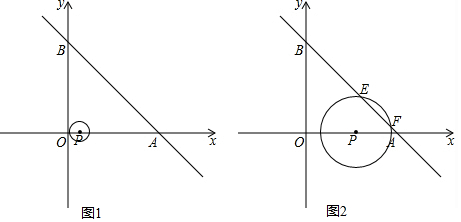
如图1,一次函数y=-x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时P的半径以每秒增加1个单位的速度不断变大,设运动
题目详情
如图1,一次函数y=-x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的 P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时 P的半径以每秒增加1个单位的速度不断变大,设运动时间为t(s)
(1)点A的坐标为___,点B的坐标为___,∠OAB=___°;
(2)在运动过程中,点P的坐标为___, P的半径为___(用含t的代数式表示);
(3)当 P与直线AB相交于点E、F时
①如图2,求t=
时,弦EF的长;
②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).
(1)点A的坐标为___,点B的坐标为___,∠OAB=___°;
(2)在运动过程中,点P的坐标为___, P的半径为___(用含t的代数式表示);
(3)当 P与直线AB相交于点E、F时
①如图2,求t=
| 5 |
| 2 |
②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).

▼优质解答
答案和解析
(1)∵y=-x+10的图象交x轴于点A,交y轴于点B,
∴A(10,0),B(0,10),
∴OA=OB=10,
∵∠AOB=90°,
∴∠OAB=∠OBA=45°,
故答案分别为(10,0),(0,10),45°.
(2)由题意P(1+2t,0), O半径为1+t,
故答案分别为(1+2t,0),1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.
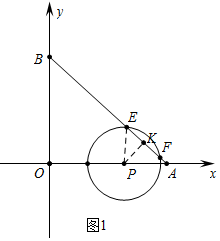
当t=
时,P(6,0),半径为3.5,
在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,
∴PK=
PA=2
,
在Rt△PEK中,EK=
=
,
∴EF=2EK=
.
②存在.
a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°
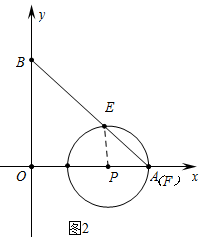
∵OP+PA=OA,
∴1+2t+1+t=10,
∴t=
.
b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.
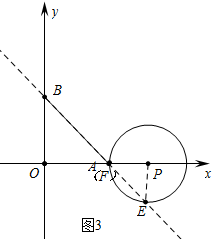
由OP-PF=OA,
∴1+2t-(1+t)=10,
∴t=10,
综上所述,t=
s或10s时,存在以点P为直角顶点的Rt△PEF.
∴A(10,0),B(0,10),
∴OA=OB=10,
∵∠AOB=90°,
∴∠OAB=∠OBA=45°,
故答案分别为(10,0),(0,10),45°.
(2)由题意P(1+2t,0), O半径为1+t,
故答案分别为(1+2t,0),1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.

当t=
| 5 |
| 2 |
在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,
∴PK=
| ||
| 2 |
| 2 |
在Rt△PEK中,EK=
| PE2-PK2 |
| ||
| 2 |
∴EF=2EK=
| 17 |
②存在.
a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°

∵OP+PA=OA,
∴1+2t+1+t=10,
∴t=
| 8 |
| 3 |
b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.

由OP-PF=OA,
∴1+2t-(1+t)=10,
∴t=10,
综上所述,t=
| 8 |
| 3 |
看了 如图1,一次函数y=-x+1...的网友还看了以下:
已知直线L的函数关系式是y=-4/3+8,且L与x轴,y轴交于A、B,动点Q从B点开始在线段BA上以 2020-03-30 …
直角坐标系中,点A在x轴上,点B在y轴上,∠BAO=60°,AC平分∠BAO交y轴于点C,若AC= 2020-05-14 …
已知数轴上点A原点左侧,距原点2个单位长度,点A向右移动12个单位长度到达点B的位置若点P、Q分别 2020-05-15 …
数轴上两点A、B对应的数是-10,30啊点P从A点出发,沿数轴正方向以1单位长度/秒的速度匀速平移 2020-05-16 …
数轴上A、B对应的数为-10、30,点P从A点出发,沿数轴正方向以1单位长度/秒的速度匀(1)当P 2020-05-16 …
如图,已知A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12.(1)写出数轴上点A、B 2020-06-13 …
已知数轴上两点A,B对应的数分别为-2,4,P为数轴上一动点,对应的数为x.(1)若P为线段AB的 2020-06-27 …
如图1,一次函数y=-x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的P与y轴相切 2020-07-17 …
如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.(1)写出数轴上 2020-07-29 …
如图,在数轴上点A表示的有理数为-4,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度 2020-07-31 …