10个学生排成一行，老师想要为每个学生配一顶帽子，帽子有两种颜色：红色和白色，每种颜色的帽子数量都超过10顶．要求：任意多个连续相邻的学生里戴红帽子与戴白帽子的人数之差最多

Question

10个学生排成一行，老师想要为每个学生配一顶帽子，帽子有两种颜色：红色和白色，每种颜色的帽子数量都超过10顶．要求：任意多个连续相邻的学生里戴红帽子与戴白帽子的人数之差最多为2．那么老师有___种分配帽子的方法．

Answer 1

本题难度很大，主要在“任意多个连续相邻的学生里戴红帽子与戴白帽子的人数之差最多为 2”这句话．以下尝试几种方法来解答．（统一用√表示带红色帽子，×表示白色帽子）
法一：有序枚举，结合图形标数法

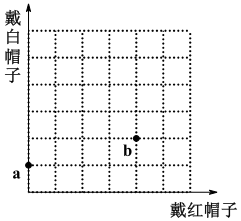
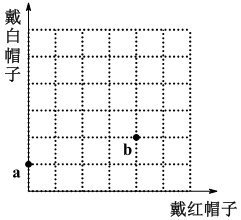
向右一格表示戴红帽子，向上一格代表戴白帽子，一共走 10 格完成注意：①同方向最多连续两步；②取的点之间，任意两个点在横方向和竖方向的格子数差最多为 2，如图 a 点和 b 点不能同时有．（行列 1×4，2×5，3×6 都不行，易多数）这样数下来，就是下面 47 种：

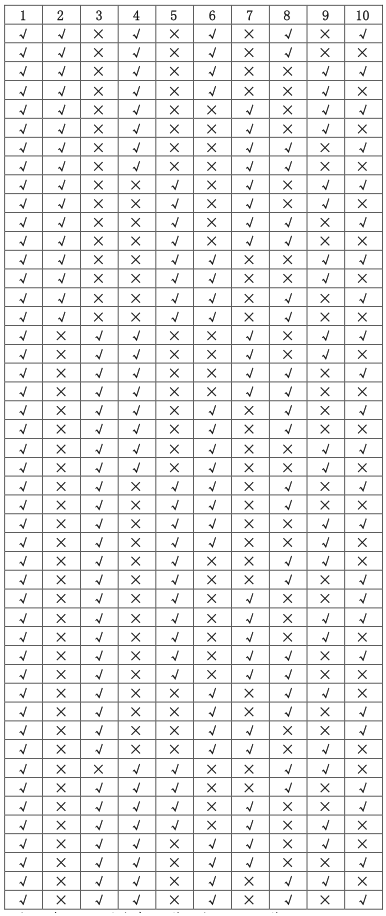
这是√开头的，共 47 中，×开头也有 47 种，共 47×2=94 种．
法二：分类讨论+枚举
根据“任意多个连续相邻的学生里戴红帽子与戴白帽子的人数之差最多为 2”，那么全部 10 名学生里戴红帽子与戴白帽子的人数之差最多也为 2，因此有 6 红 4 白，5 红 5 白，4 红 6 白三种．其中 6 红 4 白和 4 红 6 白对称，种数一样．
（一）6 红 4 白
（1）6 红分三堆，红红，红红，红红
4-2=2，红红与红红之间必为两白，1 种：
√√，××，√√，××，√√；
小计，6 红分三堆共 1 种；
（2）6 红分四堆，红红，红红，红，红
①红红，红红，红，红红红与红红之间必为两白，1 种：
√√，××，√√，×，√，×，√；
②红，红，红红，红红同①，对称性，1 种；
③红红，红，红红，红
5-2=3，这两个间隔里必然一个是 1 白，一个是两白，2 种：
√√，××，√，×，√√，×，√；
√√，×，√，××，√√，×，√；
④红，红红，红，红红同③，2 种
⑤红红，红，红，红红
6-2=4，两端必然不可能放白，3 种：
√√，××，√，×，√，×，√√；
√√，×，√，××，√，×，√√；
√√，×，√，×，√，××，√√；
⑥红，红红，红红，红红红与红红之间必为两白，1 种：
√，×，√√，××，√√，×，√；
小计，6 红分四堆共 1+1+2+2+3+1=10 种；
（3）6 红分五堆，红红，红，红，红，红
①红红在第一或第五位置，四个间隔各插 1 白，共 2 种：
√√，×，√，×，√，×，√，×，√；
√√，×，√，×，√，×，√，×，√；
②红红在第二、三、四位置，四个间隔各插 1 白，共 3 种：
√，×，√√，×，√，×，√，×，√；
√，×，√，×，√√，×，√，×，√；√，×，√，×，√，×，√√，×，√；
小计，6 红分五堆共 2+3=5 种；所以，6 红 4 白共 1+10+5=16 种；
（二）4 红 6 白
同 6 红 4 白，共 16 种；
（三）5 红 5 白
（1）5 红分三堆，红红，红红，红
①红红，红红，红
第一个间隔红红与红红之间必为两白，第二个间隔可能 1 白，可能两白，5 种：
×，√√，××，√√，××，√；
√√，××，√√，××，√，×；
√√，××，√√，×，√，××；
××，√√，××，√√，×，√；
×，√√，××，√√，×，√，×．
③红红，红，红红
5-2=3，1+2=3，划线处两间隔必为一处 1 白，一处两白，6 种：
××，√√，××，√，×，√√；
√√，××，√，×，√√，××；
×，√√，××，√，×，√√，×；
××，√√，×，√，××，√√；
√√，×，√，××，√√，××；
×，√√，×，√，××，√√，×；
小计，5 红分三堆共 5+5+6=16 种；
（2）5 红分四堆，红红，红，红，红
①红红，红，红，红
1+2=3，2+2=4，划线处三个间隔为 3 到 4 白，9 种：
×，√√，××，√，×，√，×，√；
√√，××，√，×，√，×，√，×；
×，√√，×，√，××，√，×，√；
√√，×，√，××，√，×，√，×；
×，√√，×，√，×，√，××，√；
√√，×，√，×，√，××，√，×；
××，√√，×，√，×，√，×，√；
√√，×，√，×，√，×，√，××；
×，√√，×，√，×，√，×，√，×；
②红，红，红，红红
同①，对称性，9 种；③红，红红，红，红
1+2=3，红两边间隔处最多一处为两白，根据三处间隔两白数量可为 2，1，0 枚举，
11 种：
√，××，√√，××，√，×，√，；
√，××，√√，×，√，××，√，；
×，√，××，√√，×，√，×，√；
√，××，√√，×，√，×，√，×；
×，√，×，√√，××，√，×，√；
√，×，√√，××，√，×，√，×；
×，√，×，√√，×，√，××，√；
√，×，√√，×，√，××，√，×；
××，√，×，√√，×，√，×，√；
√，×，√√，×，√，×，√，××；
×，√，×，√√，×，√，×，√，×；
④红，红，红红，红同③，11 种；
小计，5 红分四堆共 9+9+11+11=40 种
（3）5 红分五堆，红，红，红，红，红，四个间隔各用 1 白，还剩 1 白有 6 处可放，6 种：
×，√，×，√，×，√，×，√，×，√；
√，××，√，×，√，×，√，×，√；
√，×，√，××，√，×，√，×，√；
√，×，√，×，√，××，√，×，√；
√，×，√，×，√，×，√，××，√；
√，×，√，×，√，×，√，×，√，×；
小计，5 红分五堆共 6 种；
所以，5 红 5 白共 16+40+6=62 种；
综上，共 16+16+62=94 种．