如图，正方形ABCD中，以AD为底边作等腰△ADE，将△ADE沿DE折叠，点A落到点F处，连接EF刚好经过点C，再连接AF，分别交DE于G，交CD于H．在下列结论中：①△ABM≌△DCN；②∠DAF=30°；③△AEF是等

Question

如图，正方形ABCD中，以AD为底边作等腰△ADE，将△ADE沿DE折叠，点A落到点F处，连接EF刚好经过点C，再连接AF，分别交DE于G，交CD于H．在下列结论中：
①△ABM≌△DCN；②∠DAF=30°；③△AEF是等腰直角三角形；④EC=CF；⑤S_△HCF=S_△ADH，
其中正确的结论有（　　）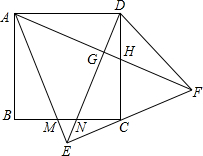

A. 2个

B. 3个

C. 4个

D. 5个

Answer 1

如图，连接AC、以D为圆心DA为半径画圆．
∵四边形ABCD是正方形，
∴DA=DC=AB=BC，∠ADC=∠B=∠DCB=90°，∠ACD=∠DAC=45°
∵△DEF是由△DEA翻折得到，
∴DA=DF=DC，EA=EF，∠AED=∠DEF，
∴∠AFC=(1)/(2)∠ADC=45°
∴∠EFA=∠EAF=45°，
∴∠AEF=90°，
∴∠DEF=∠DEA=45°，
∵EA=ED=EF，
∴∠DAE=∠ADE=∠EDF=∠EFD=67.5°，
∴∠DAF=∠DFA=22.5°，
∴∠ADF=180°-∠DAF-∠DFA=135°，
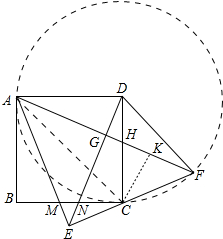
∴∠CDF=∠ADF-∠ADC=45°，
∴∠DCF=180°-∠CDF-∠DFC=67.5°，
∵∠CHF=∠CDF+∠DFA=67.5°，
∴∠HCF=∠FHC，
∴△CFH是等腰三角形，故③正确．②错误，
∵∠ACD=∠CDF，
∴AC∥DF，
∴S_△DFA=S_△FDC，
∴S_△ADH=S_△CHF，故⑤正确，
∵EA=ED，
∴∠EAD=∠EDA，
∴∠BAM=∠CDN，
在△ABM和△DCN中，

∠BAM=∠CDN

AB=DC

∠B=∠DCN

，
∴△ABM≌△DCN，故①正确，
在△EAF中，∵∠CAE=∠CAF，∠AEC=90°，作CK⊥AF于K，
∴CE=CK<CF，
∴CE≠CF故④错误．
∴①③⑤正确，
选B．