早教吧作业答案频道 -->数学-->
已知△ABC中,∠ABC=∠ACB,D为射线CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.(1)如图(1),①若∠BAC=40°,∠DAE=30°,则α=,β=.②写出α与
题目详情
已知△ABC中,∠ABC=∠ACB,D为射线CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
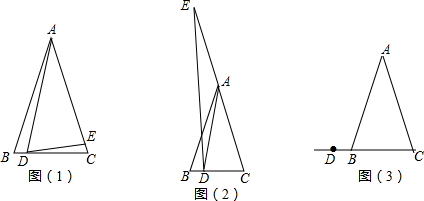
(1)如图(1),
①若∠BAC=40°,∠DAE=30°,则α=___,β=___.
②写出α与β的数量关系,并说明理由;
(2)如图(2),当D点在BC边上,E点在CA的延长线上时,其它条件不变,写出α与β的数量关系,并说明理由.
(3)如图(3),D在CB的延长线上,根据已知补全图形,并直接写出α与β的关系式___.
(1)如图(1),
①若∠BAC=40°,∠DAE=30°,则α=___,β=___.
②写出α与β的数量关系,并说明理由;
(2)如图(2),当D点在BC边上,E点在CA的延长线上时,其它条件不变,写出α与β的数量关系,并说明理由.
(3)如图(3),D在CB的延长线上,根据已知补全图形,并直接写出α与β的关系式___.

▼优质解答
答案和解析
(1)①α=10°,β=5°;
故答案为:10°,5°;
②α=2β,
设∠BAC=x°,∠DAE=y°,则α=x°-y°
∵∠ABC=∠ACB
∴∠C=
∵∠ADE=∠AED
∴∠AED=
∴β=
-
=
∴α=2β;
(2)β=
,
设∠BAC=x°,∠DAE=y°,则∠CAD=180°-y°
∴α=x°-(180°-y°)=x°-180°+y°
∵∠ABC=∠ACB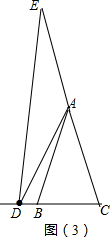
∴∠C=
∵∠ADE=∠AED
∴∠AED=
∴β=180°-
-
=
∴β=
;
(3)如图,β=
,
设∠BAC=x°,∠DAE=y°,则∠CAD=180°-y°
∴α=180°-y°-x°=180°-y°-x°,
∵∠ABC=∠ACB
∴∠C=
∵∠ADE=∠AED
∴∠AED=
,∴
∴β=180°-
-
=
∴β=
.
故答案为:β=
.
故答案为:10°,5°;
②α=2β,
设∠BAC=x°,∠DAE=y°,则α=x°-y°
∵∠ABC=∠ACB
∴∠C=
| 180°-x° |
| 2 |
∵∠ADE=∠AED
∴∠AED=
| 180°-y° |
| 2 |
∴β=
| 180°-y° |
| 2 |
| 180°-x° |
| 2 |
| x°-y° |
| 2 |
∴α=2β;
(2)β=
| 180°+α |
| 2 |
设∠BAC=x°,∠DAE=y°,则∠CAD=180°-y°
∴α=x°-(180°-y°)=x°-180°+y°
∵∠ABC=∠ACB

∴∠C=
| 180°-x° |
| 2 |
∵∠ADE=∠AED
∴∠AED=
| 180°-y° |
| 2 |
∴β=180°-
| 180°-y° |
| 2 |
| 180°-x° |
| 2 |
| x°+y° |
| 2 |
∴β=
| 180°+α |
| 2 |
(3)如图,β=
| 180°-α |
| 2 |
设∠BAC=x°,∠DAE=y°,则∠CAD=180°-y°
∴α=180°-y°-x°=180°-y°-x°,
∵∠ABC=∠ACB
∴∠C=
| 180°-x° |
| 2 |
∵∠ADE=∠AED
∴∠AED=
| 180°-y° |
| 2 |
∴β=180°-
| 180°-y° |
| 2 |
| 180°-x° |
| 2 |
| x°+y° |
| 2 |
∴β=
| 180°-α |
| 2 |
故答案为:β=
| 180°-α |
| 2 |
看了 已知△ABC中,∠ABC=∠...的网友还看了以下:
已知a是3个正数a.b.c中最大的数,且a/b=c/d,则a+d于c+d的大小关系是?(则a+d于c 2020-03-31 …
读图完成问题1.位于东西半球分界线上的点是2.同时位于东半球、北半球、中纬度的点有A.F点B.D点 2020-04-23 …
有a、b、c、d、e、f、g七种物质.a为HCl,f的元素质量比为7:3.a能与b、f、d反应,c 2020-05-02 …
已知a向量=(1,2),b向量=(3,-4),c向量=a向量+(x-3)b向量,d向量=-ya向量 2020-06-06 …
请在坐标系中描出下列各点:A(2,1),B(2,-3),C(-1,2),D(3,2),E(3,3) 2020-06-25 …
C语言问题#includevoidmain(){inta=3,C语言问题#includevoidm 2020-07-23 …
a,b,c,d表示4个有理数,已知其中每三个数之和如下:a+b+c=1,a+b+d=-3,a+c+d 2020-11-03 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
将a=-8,b=3,c=2,d=-4分别带入下面两个式子计算结果看看他们是否相等(a-b)-(c-d 2020-12-31 …
常温下,向稀Na2CO3溶液中加水,下列数值增大的是()A.c(OH-)B.c(Na+)c(CO2- 2021-01-12 …