已知球O是正三棱锥（底面为正三角形，顶点在底面的射影为底面中心）A-BCD的外接球，BC=3，AB=23，点E在线段BD上，且BD=3BE，过点E作圆O的截面，则所得截面圆面积的取值范围是（）A.[π

Question

已知球O是正三棱锥（底面为正三角形，顶点在底面的射影为底面中心）A-BCD的外接球，BC=3，AB=2

√(3)，点E在线段BD上，且BD=3BE，过点E作圆O的截面，则所得截面圆面积的取值范围是（　　）

A. [π，4π]

B. [2π，4π]

C. [3π，4π]

D. （0，4π]

Answer 1

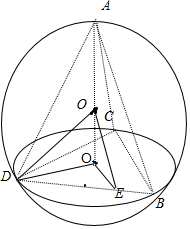如图，设△BDC的中心为O₁，球O的半径为R，
连接oO₁D，OD，O₁E，OE，
则O1D=3sin600×(2)/(3)=√(3)，AO₁=√(AD2-DO12)=3，
在Rt△OO₁D中，R²=3+（3-R）²，解得R=2，
∵BD=3BE，∴DE=2
在△DEO₁中，O₁E=√(3+4-2×√(3)×2×cos300)=1
∴OE=√(O1E2+OO12)=√(2)
过点E作圆O的截面，当截面与OE垂直时，截面的面积最小，此时截面圆的半径为√(22-(√(2))2)=√(2)，最小面积为2π
当截面过球心时，截面面积最大，最大面积为4π．
故选：B．