早教吧作业答案频道 -->数学-->
若以三角形的一边为边向形外作正三角形,以这边所对两个顶点为端点的线段称这个三角形的奇异线.如图1,以△ABC的边BC为边,向外作正△BCD,则AD是△ABC的一条奇异线.(1)如图2,CD,A
题目详情
若以三角形的一边为边向形外作正三角形,以这边所对两个顶点为端点的线段称这个三角形的奇异线.
如图1,以△ABC的边BC为边,向外作正△BCD,则AD是△ABC的一条奇异线.
(1)如图2,CD,AE都是△ABC的奇异线,求证:CD=AE;
(2)如图3,△ABC内接于 O,BD是它的奇异线,且点D在 O上,
①直接写出∠ABC=___度.
②若AB=2,BC=3,求奇异线BD的长.
(3)若图1△ABC中,∠BAC=30°,AB=
,AC=
,求△ABC的奇异线AD的长.
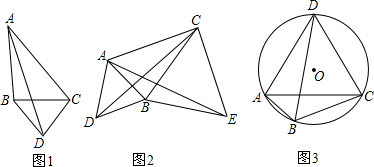
如图1,以△ABC的边BC为边,向外作正△BCD,则AD是△ABC的一条奇异线.
(1)如图2,CD,AE都是△ABC的奇异线,求证:CD=AE;
(2)如图3,△ABC内接于 O,BD是它的奇异线,且点D在 O上,
①直接写出∠ABC=___度.
②若AB=2,BC=3,求奇异线BD的长.
(3)若图1△ABC中,∠BAC=30°,AB=
| | 2 |
| | 3 |

▼优质解答
答案和解析
(1)证明:如图2,由题意可得:△ABD、△BCE为正三角形,
∴AB=DB,BC=BE,
∠ABD=∠CBE=60°,
∴∠ABD+∠ABC=∠CBE+∠ABC,
即∠DBC=∠ABE;
在△DBC和△ABE中
∵
,
∴△DBC≌△ABE(SAS),
∴CD=AE;
(2) ①如图3,∵∠ADC=60°,
∴∠ABC=120°,
故答案为:120;
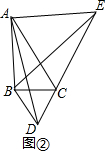
②如图①,
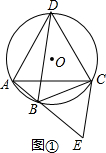
以BC为边向外作正△BCE,则BD=AE,
∴∠CBE=120°+60°=180°,
∴A,B,E在同一直线上,
∴BD=AE=AB+BE=AB+BC=2=3=5,
(3) 如图②,
以AC为边向外作正△ACE,则AD=BE,
在△ABE中,∠BAE=∠BAC+∠CAE=30°+60°=90°,
∵AB=
,AE=AC=
,
∴BE=
=
,
∴AD=BE=
.
∴AB=DB,BC=BE,
∠ABD=∠CBE=60°,
∴∠ABD+∠ABC=∠CBE+∠ABC,
即∠DBC=∠ABE;
在△DBC和△ABE中
∵
|
∴△DBC≌△ABE(SAS),
∴CD=AE;
(2) ①如图3,∵∠ADC=60°,
∴∠ABC=120°,
故答案为:120;
②如图①,
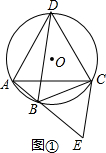
以BC为边向外作正△BCE,则BD=AE,
∴∠CBE=120°+60°=180°,
∴A,B,E在同一直线上,
∴BD=AE=AB+BE=AB+BC=2=3=5,
(3) 如图②,

以AC为边向外作正△ACE,则AD=BE,
在△ABE中,∠BAE=∠BAC+∠CAE=30°+60°=90°,
∵AB=
| 2 |
| 3 |
∴BE=
| AB2+AE2 |
| 5 |
∴AD=BE=
| 5 |
看了 若以三角形的一边为边向形外作...的网友还看了以下:
两根木条,一根长20厘米,另一根长50厘米,将它们的一段重合,放在同一条直线上,此时两根木条的中点间 2020-03-30 …
两根木条'一根长20厘米,一根长24厘米,将它们一端重合,且放在同一条直纸上,求此时两根木条的中点之 2020-03-30 …
两根木条,一根长20厘米,一根长24厘米,将它们一端重合,且放在同一条直线上,求此时两根木条的中点之 2020-03-30 …
题目是两根木条,一根长60cm,一根长100cm,将他们的一端重合,放在同一条直线上,此时两根木条的 2020-03-31 …
已知两根木条,一根长60cm,一根长100cm,将它们的一端重合,放在同一条直线上,此时两根木条的中 2020-03-31 …
有两根木条,一根长60厘米,一根长100厘米.如果将它们放在同一条直线上,并且使一个端点重合,这两 2020-05-20 …
两根木条一根长80cm,一根长120cm,将它们的一端重合,顺次放在同一条直线上,此时两根木条的中 2020-05-21 …
求24点数学题目和解决方法,不下于20条,明天中午之前回答,按回答程度加悬赏.是这样的,我去参加别 2020-05-22 …
一道数学题:两根木条,一根长40cm,一根长20cm.两根木条,一根长40cm,一根长20cm,将 2020-06-02 …
有理数算24点使横竖交叉都等于24-379-8546-4-73561-3710要横竖和交叉每一条的 2020-06-03 …