早教吧作业答案频道 -->数学-->
(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)(2)应用:点A为线段BC外一动点,且BC=3,AB=1,
题目详情
(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于___时,线段AC的长取得最大值,且最大值为___(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.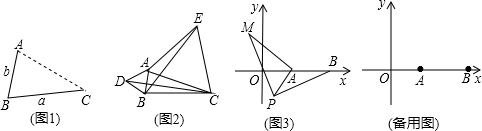
填空:当点A位于___时,线段AC的长取得最大值,且最大值为___(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.

▼优质解答
答案和解析
(1)∵点A为线段BC外一动点,且BC=a,AB=b,
∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b,
故答案为:CB的延长线上,a+b;
(2)①CD=BE,
理由:∵△ABD与△ACE是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△CAD与△EAB中,
,
∴△CAD≌△EAB,
∴CD=BE;
②∵线段BE长的最大值=线段CD的最大值,
由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,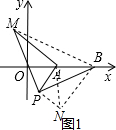
∴最大值为BD+BC=AB+BC=4;
(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,
则△APN是等腰直角三角形,
∴PN=PA=2,BN=AM,
∵A的坐标为(2,0),点B的坐标为(5,0),
∴OA=2,OB=5,
∴AB=3,
∴线段AM长的最大值=线段BN长的最大值,
∴当N在线段BA的延长线时,线段BN取得最大值,
最大值=AB+AN,
∵AN=
AP=2
,
∴最大值为2
+3;
如图2,过P作PE⊥x轴于E,
∵△APN是等腰直角三角形,
∴PE=AE=
,
∴OE=BO-
-3=2-
,
∴P(2-
,
).
∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b,
故答案为:CB的延长线上,a+b;
(2)①CD=BE,
理由:∵△ABD与△ACE是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△CAD与△EAB中,
|
∴△CAD≌△EAB,
∴CD=BE;
②∵线段BE长的最大值=线段CD的最大值,
由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,

∴最大值为BD+BC=AB+BC=4;
(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,
则△APN是等腰直角三角形,
∴PN=PA=2,BN=AM,
∵A的坐标为(2,0),点B的坐标为(5,0),
∴OA=2,OB=5,
∴AB=3,

∴线段AM长的最大值=线段BN长的最大值,
∴当N在线段BA的延长线时,线段BN取得最大值,
最大值=AB+AN,
∵AN=
| 2 |
| 2 |
∴最大值为2
| 2 |
如图2,过P作PE⊥x轴于E,
∵△APN是等腰直角三角形,
∴PE=AE=
| 2 |
∴OE=BO-
| 2 |
| 2 |
∴P(2-
| 2 |
| 2 |
看了 (1)发现:如图1,点A为线...的网友还看了以下:
植物茎秆柔弱容易倒伏,是由于土壤中缺少哪种无机盐所致?()A.含氮的B.含磷的C.含钾的D.含钙的 2020-04-06 …
请根据自己的积累,写出下列加点的字含义相同的成语.例子:齐人三鼓的鼓----一鼓作气 1.彼竭我盈 2020-05-16 …
请根据自己的积累,写出下列加点的字含义相同的成语.例子:齐人三鼓的鼓----一鼓作气 1.彼竭我盈 2020-05-16 …
假如10点的聚羧酸减水剂2.0的掺量,减水率是20.那20点的固含1.0的掺量,减水率也是20吗? 2020-06-19 …
一道文言文选择题今晚就要感激不尽啊!1.下列句子中加点的词含义相同的一项是()A.养之成群之/恐众 2020-07-01 …
下列关于细菌的叙述中,不正确的是()A.DNA是裸露的B.含有细胞壁和鞭毛C.含有核膜包被的细胞核 2020-07-04 …
醛类是重要的有机物.(1)松柏醇臭氧化反应生成的B含有醛基.写出结构简式:B;A.(2)已知:①C 2020-07-05 …
图甲表示细胞中ATP反应链,图中a、b、c代表酶,A、B、C代表化合物;图乙表示酶活性与温度的关系 2020-07-21 …
关于磁感应强度,正确的说法是()A.根据定义式B=FIL,磁场中某点的磁感应强度B与F成正比,与IL 2020-10-30 …
巴尔扎克说:“只有那些晓得控制他们缺点,不让这些缺点控制自己的人,才是强者。”这句话告诉我们()A. 2020-12-14 …