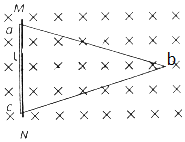
如图所示，等腰三角形导线框abc固定在匀强磁场中，ac长为l，ab长度为2514l，导线电阻可不计．磁场的磁感应强度为B，方向垂直于纸面向里．现有一段长度为l、电阻为R的均匀导体杆MN架在导

Question

如图所示，等腰三角形导线框abc固定在匀强磁场中，ac长为l，ab长度为(25)/(14)l，导线电阻可不计．磁场的磁感应强度为B，方向垂直于纸面向里．现有一段长度为l、电阻为R的均匀导体杆MN架在导线框上，开始时紧靠ac，然后沿垂直于ac方向以初速度v向b端滑动，滑动中始终与ac平行并与导线保持良好接触，所有摩擦不计，当MN滑过的距离为(4)/(7)l时，导体杆MN的速度变为(v)/(2)，问杆MN能不能滑离导线框abc？若能，求出滑杆MN杆刚滑离导线框时的速度；若不能，求杆停止运动时到ac的距离．（提示：应用动量定理F△t=m△v）

Answer 1

导体棒滑动过程中切割的长度为l’，则此时接入电路的电阻R'=(l′)/(l)R；
感应电动势E=Bl'v；
由欧姆定律可知，感应电流I=(E)/(R′)
联立解得：I=(BLv)/(R)
则对滑过的(4)/(7)l过程由动量定理可得：
-BIL△t=△mv
则有：
(B2l2v△t)/(R)=△mv
则对前(4)/(7)l综合分析可有：
(B2l2)/(R)×(4)/(7)l=(mv)/(2)
解得：
(8B2l3)/(7R)=mv  ①
假设导体棒静止在框架上，则对全程由动量定理可得：
-(B2L2x)/(R)=-mv  ②
联立①、②可得：
x=(8l)/(7)；
由几何关系可知，导体框的总长度为：d=√(((25)/(14)l)2-((l)/(2))2)≈1.7L>(8L)/(7)，故说明MN不能脱离导体框，静止时离框的距离为(8l)/(7)．
答：杆不能离开导体框，停止运动时到ac的距离为(8l)/(7)