某单位280名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如

Question

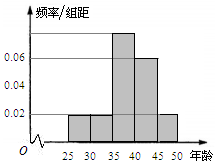
某单位280名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．
（ I）现要从年龄低于40岁的员工中用分层抽样的方法抽取12人，则年龄在第1，2，3组的员工人数分别是多少？
（ II）为了交流读书心得，现从上述12人中再随机抽取3人发言，设3人中年龄在[35，40）的人数为ξ，求ξ的数学期望；
（ III）为了估计该单位员工的阅读倾向，现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查，调查结果如下表所示：（单位：人）

	喜欢阅读国学类	不喜欢阅读国学类	合计
男	14	4	18
女	8	14	22
合计	22	18	40

根据表中数据，我们能否有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系？
附：K2=(n(ad-bc)2)/((a+b)(c+d)(a+c)(b+d))，其中n=a+b+c+d

P（K2≥k0）	0.05	0.025	0.010	0.005	0.001
k0	3.841	5.024	6.635	7.879	10.828

Answer 1

（Ⅰ）由频率分布直方图得前三组的人数分别为：0.02×5×280=28，28，
[1-（0.02+0.02+0.06+0.02）×5]×280=112
所以前三组抽取的人数分别为(28)/(28+28+112)×12=2，2，8（3分）
（ II）由上可知，ξ的所有可能取值为0，1，2，3，其概率分别为P(ξ=0)=(C34)/(C312)=(1)/(55)，P(ξ=1)=(C18C24)/(C312)=(12)/(55)P(ξ=2)=(C28C14)/(C312)=(28)/(55)，P(ξ=3)=(C38)/(C312)=(14)/(55)（7分）
所以，Eξ=0×(1)/(55)+1×(12)/(55)+2×(28)/(55)+3×(14)/(55)=2（9分）
（Ⅲ）假设H₀：“是否喜欢看国学类书籍和性别无关系”，根据表中数据，
求得K²的观测值k=(40×(14×14-4×8)2)/(22×18×22×18)≈6.8605>6.635，（11分）
查表得P（K²≥6.635）=0.01，从而能有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系（12分）