国庆长假期间小明去参观画展，为了保护壁画，举办方在壁画前方用垂直于地面的透明玻璃幕墙与观众隔开，小明在一幅壁画正前方驻足观看．如图是小明观看该壁画的纵截面示意图

Question

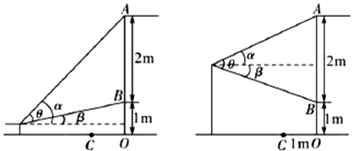国庆长假期间小明去参观画展，为了保护壁画，举办方在壁画前方用垂直于地面的透明玻璃幕墙与观众隔开，小明在一幅壁画正前方驻足观看．如图是小明观看该壁画的纵截面示意图，已知壁画高度AB是2米，壁画底端与地面的距离BO是1米，玻璃幕墙与壁画之间的距离OC是1米．若小明的身高为a米（0＜a＜3），他在壁画正前方x米处观看，问x为多少时，小明观看这幅壁画上下两端所成的视角θ最大？

Answer 1

（本小题满分16分）因为y=tanx在x∈（0，）是增函数，（1）当0＜a＜1时，如图1，tanθ=tan（α-β）==，令函数f（x）=，可证明函数f（x）在（0，）是单调减函数，在是单调增函数．若时，即，f（x）在[1，+∞）上是增函数，此时当x=1时tanθ取得最大值，则视角θ最大．若时，即，①当x=时，tanθ取得最大值，则视角θ最大．②当a=1时，tanθ=（x≥1），当x=1时tanθ取得最大值，则视角θ最大．（2）当1＜a＜3且a≠2时如图2，tanθ═tan（α+β）==，令g（x）=，在[1，+∞）上是增函数，所以当x=1时，ymax＞0，tanθ＞0，故θ为锐角．∴当x=1时，g（x）取得最小值，tanθ取得最大值，则视角θ最大．综上：当时，且x=1时，视角θ最大；当，时，且x=时，视角θ最大．
分析：
通过0＜a＜1，1＜a＜3且a≠2，分别求出tanθ，构造函数通过函数的单调性求出函数的最大值，说明视角最大．
点评：
本题考查解三角形的实际应用，考查函数的单调性的应用，分类讨论思想，计算能力．