早教吧作业答案频道 -->数学-->
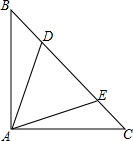
在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.
题目详情
在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.

▼优质解答
答案和解析
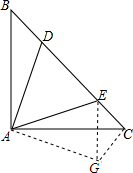 BD2+CE2=DE2,
BD2+CE2=DE2,
理由是:∵AB=AC,
∴把△ABD绕点A逆时针旋转90°至△ACG,可使AB与AC重合,连接EG,
∴AD=AG,BD=CG,∠B=∠ACG,∠BAD=∠CAG,
∵在Rt△BAC中,∠BAC=90°,AB=AC,
∴∠B=°,
∴∠ECG=∠ACB+∠ACG=∠ACB+∠B=45°+45°=90°,
∵∠BAC=90°,∠DAE=45°,
∴∠EAG=∠CAE+∠CAG=∠CAE+∠BAD=90°-45°=45°,
∴∠DAE=∠EAG,
在△DAE和△GAE中,
,
∴△DAE≌△GAE(SAS),
∴DE=EG,
在Rt△ECG中,由勾股定理得:EG2=CE2+CG2,
即BD2+CE2=DE2.
 BD2+CE2=DE2,
BD2+CE2=DE2,理由是:∵AB=AC,
∴把△ABD绕点A逆时针旋转90°至△ACG,可使AB与AC重合,连接EG,
∴AD=AG,BD=CG,∠B=∠ACG,∠BAD=∠CAG,
∵在Rt△BAC中,∠BAC=90°,AB=AC,
∴∠B=°,
∴∠ECG=∠ACB+∠ACG=∠ACB+∠B=45°+45°=90°,
∵∠BAC=90°,∠DAE=45°,
∴∠EAG=∠CAE+∠CAG=∠CAE+∠BAD=90°-45°=45°,
∴∠DAE=∠EAG,
在△DAE和△GAE中,
|
∴△DAE≌△GAE(SAS),
∴DE=EG,
在Rt△ECG中,由勾股定理得:EG2=CE2+CG2,
即BD2+CE2=DE2.
看了 在△ABC中,∠BAC=90...的网友还看了以下:
小明从A地到B地,已行的路程超过中点3/2(二分之三),剩下的路程是全程的2/5(二分之五).已行 2020-04-27 …
走一段路,已走的路程超过中点五千米,乙行的比剩下的路程多5/1,这段路有多长? 2020-04-27 …
怎样用英语写过中秋节就是用英语写下过中秋节的作文 2020-05-12 …
(分数应用题)甲,乙两车从相距360千米的A,B两地相向而行,3小时后,甲车行全程的4分之3,乙车 2020-07-15 …
初一数学二元一次方程写过程一:X-2Y=5①5X-3Y=二分之一②二:2X-Y-3=0①3X+2Y 2020-07-18 …
6分之1x+12分之1+x7分之1x+5+2分之1x+4=x解方程写过程、 2020-07-19 …
小刚把过年的压岁钱800元存入银行,存期5年.到期时,小刚从银行共取本息982.4元扣除5%的利息 2020-07-24 …
哪篇作文好在你的成长过程中肯定有成功的经历,在这个过程中你遇到哪些困难与挫折?你是怎样克服的?请选择 2020-10-30 …
1/4x+x=25解方程写过程 2020-10-31 …
算数题,有些要写过程!3/4+1/3*1/6=?要写过程6*5/8-1/2=?要写过程(1/7+1/ 2020-11-06 …