早教吧作业答案频道 -->数学-->
如图.在直四棱柱ABCD-A1B1C1D1中,E,F分別AB,BC的中点,A1C1与B1D1交于点O.(1)求证:A1,C1,F,E四点共面;(2)若底面ABCD是菱形,且OD⊥A1E,求证:OD丄平面A1C1FE.
题目详情
如图.在直四棱柱ABCD-A1B1C1D1中,E,F分別AB,BC的中点,A1C1与B1D1交于点O.
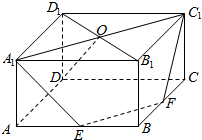
(1)求证:A1,C1,F,E四点共面;
(2)若底面ABCD是菱形,且OD⊥A1E,求证:OD丄平面A1C1FE.

(1)求证:A1,C1,F,E四点共面;
(2)若底面ABCD是菱形,且OD⊥A1E,求证:OD丄平面A1C1FE.
▼优质解答
答案和解析
(本题满分为14分)
(1)连接AC,因为E,F分别是AB,BC的中点,所以EF是△ABC的中位线,
所以EF∥AC,
由直棱柱知:AA1
CC1,所以四边形AA1C1C为平行四边形,所以AC∥A1C1,…5分
所以EF∥A1C1,
故A1,C1,F,E四点共面;…7分,
(2)连接BD,因为直棱柱中DD1⊥平面A1B1C1D1,A1C1⊂平面A1B1C1D1,
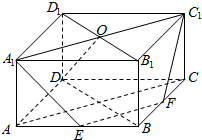 所以DD1⊥A1C1,
所以DD1⊥A1C1,
因为底面A1B1C1D1是菱形,所以A1C1⊥B1D1,
又DD1∩B1D1=D1,所以A1C1⊥平面BB1DD1,…11分
因为OD⊂平面BB1DD1,
所以OD⊥A1C1,
又OD⊥A1E,A1C1∩A1E=A1,A1C1⊂平面A1C1FE,A1E⊂平面A1C1FE,
所以OD⊥平面A1C1FE…14分
(1)连接AC,因为E,F分别是AB,BC的中点,所以EF是△ABC的中位线,
所以EF∥AC,
由直棱柱知:AA1
| ∥ |
. |
所以EF∥A1C1,
故A1,C1,F,E四点共面;…7分,
(2)连接BD,因为直棱柱中DD1⊥平面A1B1C1D1,A1C1⊂平面A1B1C1D1,
 所以DD1⊥A1C1,
所以DD1⊥A1C1,因为底面A1B1C1D1是菱形,所以A1C1⊥B1D1,
又DD1∩B1D1=D1,所以A1C1⊥平面BB1DD1,…11分
因为OD⊂平面BB1DD1,
所以OD⊥A1C1,
又OD⊥A1E,A1C1∩A1E=A1,A1C1⊂平面A1C1FE,A1E⊂平面A1C1FE,
所以OD⊥平面A1C1FE…14分
看了 如图.在直四棱柱ABCD-A...的网友还看了以下:
若a是有理数,试比较1+a与1-a的大小 2020-04-06 …
1.求满足丨x丨≤3的整数x的值2.已知2,-4,6,-8…,98,-100,求这50个数字的和3 2020-05-14 …
y=2x+1与ykx+b相交与(1,a)(1)求a的值.(2)写出y=2x+1与y=kx+b的方程 2020-06-06 …
要比较1+a与1-a的大小,首先要比较a与-a的大小而a与-a的大小由a的符号确定,故应分类讨论当 2020-06-25 …
要比较1+a与1-a的大小,首先要比较a与-a的大小,而a与-a的大小由a的符号决定,故作分类讨论 2020-06-25 …
20万火急!1:a^(1-a)与(1-a)^a;(1/2 2020-07-03 …
比较1+a与1-a的大小,首先要比较a与-a的大小而a与-a的大小由a的正负确定(1)当a>0时, 2020-07-09 …
比大小:1/(a+1)与1-a如题a属于全体实数 2020-07-13 …
设a是大于1的实数,若a,(a+2)/3,(2a+1)/31.设a是大于1的实数,若a,(a+2) 2020-07-30 …
当a>1时,取a=2,则2>1/2,取a=3/2,则3/2>2/3……所以,a>1/a.当0<a<1 2020-11-28 …