下图为一几何体的展开图.(单位:cm)（1）沿图中虚线将它们折叠起来，是哪一种特殊几何体？并请画出其直观图，比例尺是1∶2；（2）需要多少个这样的几何体才能拼成一个棱长

Question

下图为一几何体的展开图.

(单位:cm)

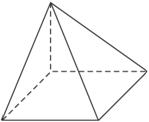
（1）沿图中虚线将它们折叠起来，是哪一种特殊几何体？并请画出其直观图，比例尺是1∶2；

（2）需要多少个这样的几何体才能拼成一个棱长为6 cm的正方体ABCD—A ₁ B ₁ C ₁ D ₁ ，请画出其示意图（需在示意图中分别表示出这种几何体）；

（3）设正方体ABCD—A ₁ B ₁ C ₁ D ₁ 的棱CC ₁ 的中点为E，试求：异面直线EB与AB ₁ 所成角的余弦值及平面AB ₁ E与平面ABC所成二面角（锐角）的余弦值．

Answer 1

（1）折叠后是有一条侧棱垂直于底面的四棱锥 直观图如下.3分      （2）需要3个这样的几何体.5分（3）①取DD1中点F，连结AF，则AF∥BE.∴∠FAB1为异面直线EB与AB1所成的角.易计算得 B1F=9，AF=3，AB1=6，7分∴cos∠FAB1===.∴异面直线EB与AB1所成角的余弦值为.②设B1E、BC的延长线交于点G，连结GA，则GA为平面AB1E与平面ABC所成二面角的棱 在底面ABC内作BH⊥AG，垂足为H.连结HB1，由三垂线定理知B1H⊥AG，∴∠B1HB为平面AB1E与平面ABC所成二面角的平面角.  在Rt△ABG中，BH==，∴HB1===.∴cos∠B1HB===.∴平面AB1E与平面ABC所成二面角的余弦值为.