早教吧作业答案频道 -->数学-->
已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.(1)求证:直线MN∥平面PBC;(2)求正四棱锥P-ABCD的表面积和体积.
题目详情
已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.
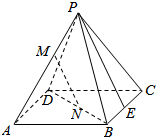
(1)求证:直线MN∥平面PBC;
(2)求正四棱锥P-ABCD的表面积和体积.

(1)求证:直线MN∥平面PBC;
(2)求正四棱锥P-ABCD的表面积和体积.
▼优质解答
答案和解析
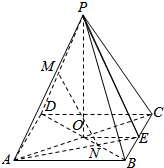 (1)证明:∵P-ABCD是正四棱锥,∴ABCD是正方形,
(1)证明:∵P-ABCD是正四棱锥,∴ABCD是正方形,
连结AN并延长交BC于点E,连结PE,
∵AD∥BC,∴EN:AN=BN:ND,
又∵BN:ND=PM:MA,∴EN:AN=PM:MA,
∴MN∥PE,
又∵PE在平面PBC内,MN在平面PBC外,
∴MN∥平面PBC.
(2) 设点P在底面ABCD上的射影为O,连结PO,
∵正四棱锥P-ABCD的底面边长及侧棱长均为13,
∴PA=AB=PB=13,OB=
=
,
由正棱锥的性质知PO=
=
,
∴正四棱锥P-ABCD的表面积:
S=4S△PAB+S正方形ABCD
=4×(
×13×13×sin60°)+13×13
=169
+169.
正四棱锥P-ABCD的体积:
V=
×S正方形ABCD×PO
=
×13×13×
=
.
 (1)证明:∵P-ABCD是正四棱锥,∴ABCD是正方形,
(1)证明:∵P-ABCD是正四棱锥,∴ABCD是正方形,连结AN并延长交BC于点E,连结PE,
∵AD∥BC,∴EN:AN=BN:ND,
又∵BN:ND=PM:MA,∴EN:AN=PM:MA,
∴MN∥PE,
又∵PE在平面PBC内,MN在平面PBC外,
∴MN∥平面PBC.
(2) 设点P在底面ABCD上的射影为O,连结PO,
∵正四棱锥P-ABCD的底面边长及侧棱长均为13,
∴PA=AB=PB=13,OB=
| 1 |
| 2 |
| 132+132 |
13
| ||
| 2 |
由正棱锥的性质知PO=
| PB2-OB2 |
13
| ||
| 2 |
∴正四棱锥P-ABCD的表面积:
S=4S△PAB+S正方形ABCD
=4×(
| 1 |
| 2 |
=169
| 3 |
正四棱锥P-ABCD的体积:
V=
| 1 |
| 3 |
=
| 1 |
| 3 |
13
| ||
| 2 |
=
2197
| ||
| 6 |
看了 已知正四棱锥P-ABCD的底...的网友还看了以下:
利用数量积求长度已知向量a,向量b,向量c中每两个的夹角都是60度,且向量a的模=4,向量b的模= 2020-05-14 …
急,长方形面积:长86.5、宽19,求面积?长26.7,宽19.3,求面积?长30.2,宽17,求 2020-05-14 …
S是平行四边形ABCD所在平面外一点,M.N分别是SA.BD上的点,SM/MA=BN/ND.〈SM 2020-05-16 …
圆的面积等于长方体面积,求长方体的宽圆的直径是16cm,长方形的长是16cm 2020-06-02 …
如图,A是线段MN上的一点,MA,AN的长度都是正整数,B是AN的中点,若图中所有的线段总和是23 2020-07-16 …
如图,A是线段MN上一点,MA,AN的长度都是正整数,B是AN的中点,若图中所有线段之和是23,求 2020-07-16 …
在直线m上取A、B两点,已知P为线段AB的中点,点M在线段AP上,AM=6,MA=4,球MP的1. 2020-07-16 …
知道长宽比例和面积求长宽长宽比3:8面积37.72平米求长和宽 2020-07-17 …
(要写字)求缺了上面的长方体的表面积;求有两个面是正方形的长方体的表面积;已知正方体底面积和高求体积 2021-02-03 …
(要写字求缺了上面的长方体的表面积;求有两个面是正方形的长方体的表面积;已知正方体底面积和高求体积: 2021-02-03 …