某物流公司的快递车和货车同时从甲地出发，匀速向乙地行驶，快递车的速度为100km/h，货车的速度为60km/h，结果快递车比货车早2h到达乙地．快递车到达乙地后卸完物品再另装货物共用30min

Question

某物流公司的快递车和货车同时从甲地出发，匀速向乙地行驶，快递车的速度为100km/h，货车的速度为60km/h，结果快递车比货车早2h到达乙地．快递车到达乙地后卸完物品再另装货物共用30min，立即按原路以90km/h速度匀速返回，直至与货车相遇．设两车之间的距离y（km）．货车行驶时间为x（h）．
（1）求甲、乙两地之间的距离．
（2）求快递车返回时y与x之间的函数关系式．
（3）建立适当的坐标系画出y与x之间的函数图象．某物流公司的快递车和货车同时从甲地出发，匀速向乙地行驶，快递车的速度为100km/h，货车的速度为60km/h，结果快递车比货车早2h到达乙地．快递车到达乙地后卸完物品再另装货物共用30min，立即按原路以90km/h速度匀速返回，直至与货车相遇．设两车之间的距离y（km）．货车行驶时间为x（h）．
（1）求甲、乙两地之间的距离．
（2）求快递车返回时y与x之间的函数关系式．
（3）建立适当的坐标系画出y与x之间的函数图象．

Answer 1

（1）设甲、乙两地之间的距离为skm，
根据题意得：(s)/(60)-(s)/(100)=2，
解得：s=300．
答：甲、乙两地之间的距离为300km．
（2）快递车达到乙地的时间为300÷100=3（h），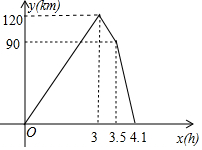
快递车离开乙地的时间为3+(1)/(2)=3(1)/(2)（h），
快递车离开乙地时，两车间的距离为300-60×3(1)/(2)=90（km），
两车相遇的时间为3(1)/(2)+90÷（60+90）=4(1)/(10)（h）．
∴快递车返回时y与x之间的函数关系式为y=90-（60+90）（x-3.5）=-150x+615（3(1)/(2)≤x≤4(1)/(10)）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示． (s)/(60)s60sss606060-(s)/(100)=2，
解得：s=300．
答：甲、乙两地之间的距离为300km．
（2）快递车达到乙地的时间为300÷100=3（h），
快递车离开乙地的时间为3+(1)/(2)=3(1)/(2)（h），
快递车离开乙地时，两车间的距离为300-60×3(1)/(2)=90（km），
两车相遇的时间为3(1)/(2)+90÷（60+90）=4(1)/(10)（h）．
∴快递车返回时y与x之间的函数关系式为y=90-（60+90）（x-3.5）=-150x+615（3(1)/(2)≤x≤4(1)/(10)）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示． (s)/(100)s100sss100100100=2，
解得：s=300．
答：甲、乙两地之间的距离为300km．
（2）快递车达到乙地的时间为300÷100=3（h），
快递车离开乙地的时间为3+(1)/(2)=3(1)/(2)（h），
快递车离开乙地时，两车间的距离为300-60×3(1)/(2)=90（km），
两车相遇的时间为3(1)/(2)+90÷（60+90）=4(1)/(10)（h）．
∴快递车返回时y与x之间的函数关系式为y=90-（60+90）（x-3.5）=-150x+615（3(1)/(2)≤x≤4(1)/(10)）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示． (1)/(2)12111222=3(1)/(2)（h），
快递车离开乙地时，两车间的距离为300-60×3(1)/(2)=90（km），
两车相遇的时间为3(1)/(2)+90÷（60+90）=4(1)/(10)（h）．
∴快递车返回时y与x之间的函数关系式为y=90-（60+90）（x-3.5）=-150x+615（3(1)/(2)≤x≤4(1)/(10)）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示． (1)/(2)12111222（h），
快递车离开乙地时，两车间的距离为300-60×3(1)/(2)=90（km），
两车相遇的时间为3(1)/(2)+90÷（60+90）=4(1)/(10)（h）．
∴快递车返回时y与x之间的函数关系式为y=90-（60+90）（x-3.5）=-150x+615（3(1)/(2)≤x≤4(1)/(10)）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示． (1)/(2)12111222=90（km），
两车相遇的时间为3(1)/(2)+90÷（60+90）=4(1)/(10)（h）．
∴快递车返回时y与x之间的函数关系式为y=90-（60+90）（x-3.5）=-150x+615（3(1)/(2)≤x≤4(1)/(10)）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示． (1)/(2)12111222+90÷（60+90）=4(1)/(10)（h）．
∴快递车返回时y与x之间的函数关系式为y=90-（60+90）（x-3.5）=-150x+615（3(1)/(2)≤x≤4(1)/(10)）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示． (1)/(10)110111101010（h）．
∴快递车返回时y与x之间的函数关系式为y=90-（60+90）（x-3.5）=-150x+615（3(1)/(2)≤x≤4(1)/(10)）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示． (1)/(2)12111222≤x≤4(1)/(10)）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示． (1)/(10)110111101010）．
（3）当x=3时，两车间的距离为300-60×3=120（km），
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示．